Perpendicular Planes

Two intersecting planes are called perpendicular planes when they form a right dihedral angle (90°).

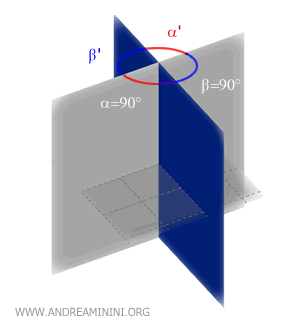
In other words, the angle between two perpendicular planes is 90° (a right angle).

So, two perpendicular planes divide space into four right dihedral regions.

They are also known as normal planes or orthogonal planes.

Perpendicular planes are distinct from oblique planes. Planes are considered oblique when they intersect but do not form a right dihedral angle, meaning their dihedral angle is not 90°.

When two planes form a right dihedral angle, they actually form three additional right dihedral angles because opposite dihedrals are congruent.

Thus, it can be said that two perpendicular planes divide three-dimensional space into four right dihedrals, each with a dihedral angle of 90°.

Conditions for Perpendicular Planes

Let’s explore how to determine whether two planes are perpendicular.

As with lines, the concept of perpendicularity between planes is based on their relative orientation: two planes are perpendicular if the angle between them is exactly 90°.

Given two planes with the following general equations: $$\pi_1: \ a x + b y + c z + d = 0 $$ $$ \pi_2: \ a' x + b' y + c' z + d' = 0 $$ the planes are perpendicular if and only if the dot product of their normal vectors equals zero: $$a \cdot a' + b \cdot b' + c \cdot c' = 0 $$

Each plane is defined by a normal vector, which is perpendicular to the plane itself:

$$ \vec{n_1} = (a, b, c) $$

$$ \vec{n_2} = (a', b', c') $$

The angle between the two planes is the same as the angle between their normal vectors.

Therefore, if the dot product of the normals is zero, the vectors are orthogonal - meaning the planes themselves are perpendicular.

Example

Consider the following two planes in general form:

$$ \pi_1: \ 2x + 3y + z - 5 = 0 $$

$$ \pi_2: \ 4x - 6y - 2z + 1 = 0 $$

Now let’s calculate the dot product of their normal vectors:

$$a \cdot a' + b \cdot b' + c \cdot c' $$

$$ (2, 3, 1) \cdot (4, -6, -2) = 2 \cdot 4 + 3 \cdot (-6) + 1 \cdot (-2) = 8 - 18 - 2 = -12 $$

Since the dot product is not zero, the two planes are not perpendicular.

Case of Explicit Equations

When the planes are written in explicit form: $$ \pi_1: \ z = m x + n y + q $$ $$ \pi_2: \ z = m' x + n' y + q' $$ the condition for perpendicularity becomes: $$ m \cdot m' + n \cdot n' = -1 $$

This formula is very similar to the condition for perpendicularity between lines in the $ xy $ plane.

In this context, the coefficients $ m $ and $ n $ represent the “slopes” of the plane with respect to the $ x $ and $ y $ axes.

Example

Consider the following two planes given in explicit form:

$$ \pi_1: \ z = 2x + 3y + 1 $$

$$ \pi_2: \ z = -\frac{1}{2}x - \frac{1}{3}y + 4 $$

We want to check whether these two planes are perpendicular.

When the equations are written as $ z = m x + n y + q $, the perpendicularity condition is:

$$ m \cdot m' + n \cdot n' = -1 $$

For the first plane we have $ m = 2 $ and $ n = 3 $; for the second plane, $ m' = -\frac{1}{2} $ and $ n' = -\frac{1}{3} $.

$$ m \cdot m' + n \cdot n' = 2 \cdot \left( -\frac{1}{2} \right) + 3 \cdot \left( -\frac{1}{3} \right) = -1 + (-1) = -2 $$

Since the result is not equal to -1,

$$ m \cdot m' + n \cdot n' = -2 \neq -1 $$

the planes are not perpendicular.

Had we found: $$ m \cdot m' + n \cdot n' = -1 $$ then the planes would indeed have been perpendicular.

And so on.