Intersection Theorem for Planes

When two distinct planes intersect in space at a point $P$, they share a line $r$ that passes through that point.

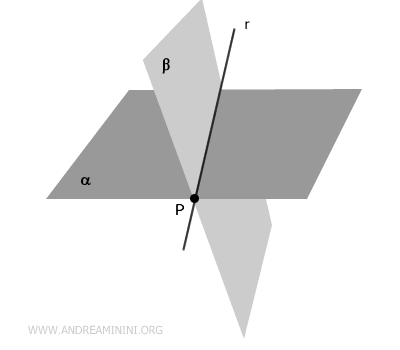
In simpler terms, two intersecting planes cannot meet at just a single point. Instead, they always share a common line.

The line shared by the two planes consists of all points that lie on both planes simultaneously.

This result stems from fundamental principles of three-dimensional geometry, which state that the intersection of two non-parallel planes in 3D space always forms a line.

Proof

Let’s examine two planes, \( \alpha \) and \( \beta \), that intersect at a point \( P \).

$$ P \in \alpha \cap \beta $$

This means that point \( P \) is part of both planes.

Next, consider two points, $A$ and $B$, that lie on the same plane $ \alpha $ but are located on opposite sides of plane $ \beta $.

Draw a line segment $ \overline{AB} $ connecting points $A$ and $B$.

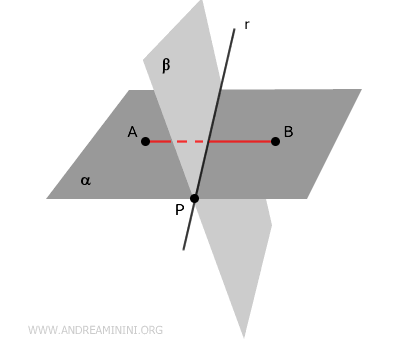
Since the planes intersect, and because the segment $ \overline{AB} $ spans across the two half-planes of $ \alpha $, it must cross plane $ \beta $ at some point $C$.

At this stage, we’ve identified two points shared by the two planes: the original point $P$ and the newly found point $C$.

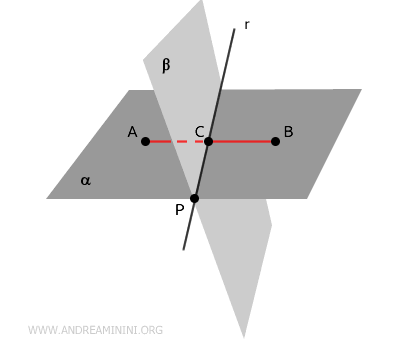
A single straight line $r$ can always be drawn through two points, and in this case, that line lies on both planes.

This proves that if two planes intersect at a single point \( P \), they must also share a line \( r \) passing through that point.

And so, the theorem is established.