Half-Plane
A half-plane is one part of a plane divided by a line, referred to as the "half-plane axis" or "origin origin/boundary of the half-plane."
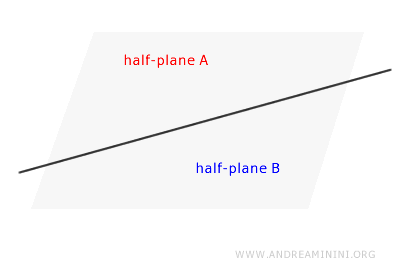
For instance, if I draw a line on a sheet of paper, I create two opposite half-planes: one to the left of the line and the other to the right.
Each half-plane is an infinite set of points. Points within a half-plane, but not on its boundary, are referred to as interior points of the half-plane.
Note: Generally, the half-plane includes both the points within one of the regions created by the division and the points on the half-plane axis itself.
Half-Plane Postulates
A half-plane must satisfy the properties of the postulate of plane partition by a line.
Given a line that splits the plane into two sets of points not on the line:
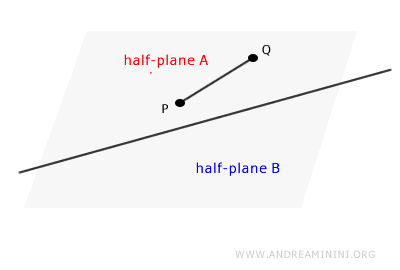
- If we consider any two points P and Q in the same region, the segment connecting them does not intersect the line.
- If we consider any two points P and Q in different regions, the segment connecting them intersects the line.
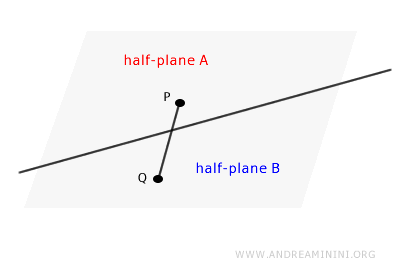
If a set of points meets this postulate, then it is considered a half-plane.
Types of Half-Planes
There are two types of half-planes:
- Open Half-Planes
An open half-plane does not include the dividing line. It consists only of the points inside the half-plane. - Closed Half-Planes
A closed half-plane includes the dividing line. It consists of both the internal points and the points on the dividing line.
Thus, in the case of a plane divided into two closed half-planes, the points on the half-plane axis are considered to belong to both half-planes.
And so on.
