Intercept Form of a Plane Equation
The intercept form of a plane equation is derived by finding the coefficients p, q, and r so that the Cartesian equation of the plane becomes $$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
The Cartesian equation of the plane is:
$$ ax+by+cz+d=0 $$
By setting y and z to zero, we get:
$$ ax+d=0 \\ ax=-d \\ x=-\frac{d}{a} $$
By setting x and z to zero, we get:
$$ by+d=0 \\ by=-d \\ y=-\frac{d}{b} $$
By setting x and y to zero, we get:
$$ cz+d=0 \\ cz=-d \\ z=-\frac{d}{c} $$
We assign the calculated values to the coefficients p, q, and r:
$$ p = -\frac{d}{a} $$
$$ q = -\frac{d}{b} $$
$$ r = -\frac{d}{c} $$
Thus, we have derived the intercept form of the plane equation:
$$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
What is the purpose of the intercept form of the plane equation?
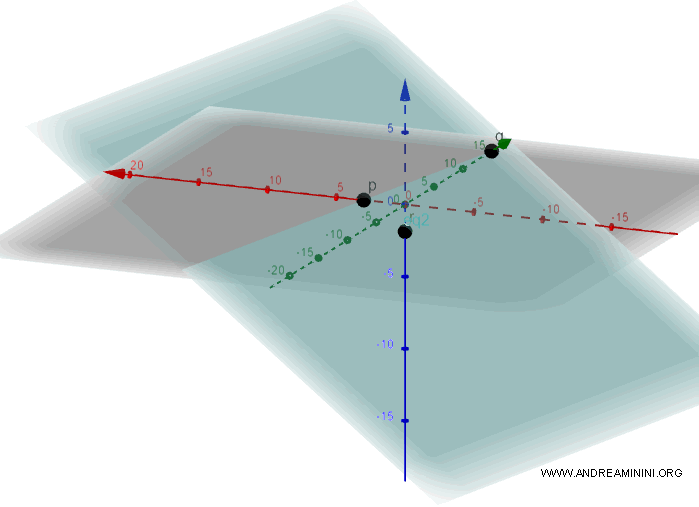
The values p, q, and r represent the points where the plane intersects the coordinate axes.
- p = intersection with the x-axis
- q = intersection with the y-axis
- r = intersection with the z-axis
A Practical Example
Consider a plane defined by the following Cartesian equation:
$$ -5x - y + 8z + 15 = 0 $$
Setting y and z to zero (y=z=0) gives the intersection point on the x-axis:
$$ -5x + 15 = 0 \\ x = \frac{15}{5} \\ x = 3 $$
Setting x and z to zero (x=z=0) gives the intersection point on the y-axis:
$$ -y + 15 = 0 \\ -y = -15 \\ y = 15 $$
Setting x and y to zero (x=y=0) gives the intersection point on the z-axis:
$$ 8z + 15 = 0 \\ 8z = -15 \\ z = -\frac{15}{8} $$
We have now found the coefficients p, q, and r for the intercept form:
$$ p = 3 $$
$$ q = 15 $$
$$ r = -\frac{15}{8} $$
Thus, the intercept form of the plane equation is:
$$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
$$ \frac{x}{3} + \frac{y}{15} + \frac{z}{-\frac{15}{8}} = 1 $$
In this form, the coefficients of the Cartesian equation represent the intersection points of the plane with the coordinate axes (x, y, z).
Note: A graphical representation of the plane and its intersection points p, q, r.