Parallel, Coincident, and Intersecting Planes in Space
Two planes in R3 can be parallel, coincident, or intersecting.
- They are parallel planes if they have no points in common.
- They are coincident planes if they are parallel and share all points.
- They are intersecting planes if they share an infinite number of points along their line of intersection.
Simply put, when planes intersect, the intersection is always a line. For parallel or coincident planes, the intersection is either nonexistent or encompasses the entire plane.
Note: Parallel and coincident planes share the same normal direction but differ in their relative positioning. In contrast, intersecting planes meet along a common line, and their normal vectors are not parallel.
How to Determine if Two Planes are Parallel, Coincident, or Intersecting
To determine if two planes in space are parallel, coincident, or intersecting, you need to analyze the linear dependence of the planes' direction vectors.
- If the vectors are linearly dependent, the planes are either parallel or coincident.
- If the vectors are linearly independent, the planes intersect.
How is the linear dependence of vectors measured?
The two planes are identified by their vector/parametric equations.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} + t_2 \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$
$$ \begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} = \begin{pmatrix} x'_0 \\ y'_0 \\ z'_0 \end{pmatrix} + t_1 \begin{pmatrix} l_3 \\ m_3 \\ n_3 \end{pmatrix} + t_2 \begin{pmatrix} l_4 \\ m_4 \\ n_4 \end{pmatrix} $$
Take the four direction vectors and arrange them in a matrix.
$$ \begin{pmatrix} l_1 & l_2 & l_3 & l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix} $$
Then calculate the rank of the matrix.
- If the rank of the matrix is equal to or less than 2, the vectors are linearly dependent. The planes are either parallel or coincident. $$ r_k \begin{pmatrix} l_1 & l_2 & l_3 & l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix} \le 2 $$
Note: To determine if the planes are parallel or coincident, check if a point from one plane also belongs to the other. If the point is on both planes, the planes are coincident. Otherwise, they are parallel.
- If the rank of the matrix is 3, the vectors are linearly independent. The planes intersect. $$ r_k \begin{pmatrix} l_1 & l_2 & l_3 & l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix} = 3 $$
So, when plane equations are expressed in parametric form, the rule to follow is as follows:
| Matrix Rank | Vector Relationship | Relative Position of the Planes |
|---|---|---|
| 1 - 2 | Linearly dependent | Either coincident or distinct parallel planes |
| 3 | Linearly independent | Intersecting planes (they meet along a line) |
The Case of Cartesian Equations
For planes with Cartesian equations
$$ a_1 x + b_1 y + c_1 z + d_1 = 0 $$
$$ a_2 x + b_2 y + c_2 z + d_2 = 0 $$
the vectors are linearly dependent if the rank of the coefficient matrix is 1.
In this case, the planes are parallel or coincident.
$$ r_k \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{pmatrix} = 1 $$
the vectors are linearly independent if the rank of the coefficient matrix is 2.
In this case, the planes intersect.
$$ r_k \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{pmatrix} = 2 $$
So, when dealing with Cartesian plane equations, the following rule applies:
| Matrix Rank | Vector Relationship | Relative Position of the Planes |
|---|---|---|
| 1 | Linearly dependent | Either coincident or distinct parallel planes |
| 2 | Linearly independent | Intersecting planes (they meet along a line) |
Example
Example 1 (Parametric Equations)
Consider two planes in space
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -1 \\ 2 \end{pmatrix} + t_2 \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -3 \\ 6 \end{pmatrix} + t_2 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} $$
Place the direction vectors into a matrix.
Then calculate the rank.
$$ r_k \begin{pmatrix} 0 & 2 & 0 & 1 \\ -1 & -1 & -3 & -1 \\ 2 & 0 & 6 & 1 \end{pmatrix} = 2 $$
The rank of the matrix is two.
Thus, the vectors are linearly dependent.
The planes are either parallel or coincident.
How to Determine if the Planes are Parallel or Coincident?
Take a point from the first plane and check if it belongs to the second.
We already know that P(0,0,0) belongs to the first plane.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -1 \\ 2 \end{pmatrix} + t_2 \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} $$
Substitute the coordinates (0,0,0) into the equation of the second plane and check if the equation is satisfied.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -3 \\ 6 \end{pmatrix} + t_2 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} $$
$$ \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -3 \\ 6 \end{pmatrix} + t_2 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} $$
Convert it into a parametric equation.
$$ \begin{cases} 0 = 0 + t_2 \\ 0 = 1 - 3t_1 - t_2 \\ 0 = 0 + 6t_1 + t_2 \end{cases} $$
$$ \begin{cases} t_2 = 0 \\ 1 - 3t_1 - (0) = 0 \\ 6t_1 + (0) = 0 \end{cases} $$
$$ \begin{cases} t_2 = 0 \\ t_1 = \frac{1}{3} \\ 6t_1 = 0 \end{cases} $$
The system has no solution.
Point P(0,0,0) does not belong to the second plane, so the planes are not coincident.
Therefore, they are parallel planes.
Example 2 (Cartesian Equations)
Consider two Cartesian equations:
$$ x + 2y + z = 0 $$
$$ 2x + 4y + 2z - 5 = 0 $$
Construct the coefficient matrix.
$$ \begin{pmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \end{pmatrix} $$
Then calculate the rank of the matrix
$$ r_k \begin{pmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \end{pmatrix} = 1 $$
The rank of the matrix is 1.
Thus, the vectors are linearly dependent, meaning they are parallel or coincident.
How to Determine if the Planes are Parallel or Coincident?
Find the coordinates of a point from the first equation by setting two coordinates to zero.
For example, let x=0 and y=0.
$$ x + 2y + z = 0 $$
$$ 0 + 20 + z = 0 $$
$$ z = 0 $$
Thus, the coordinates of a point on the first plane are:
$$ P(x, y, z) = P(0, 0, 0) $$
Substitute the coordinates of point P(0,0,0) into the equation of the second plane.
$$ 2x + 4y + 2z - 5 = 0 $$
$$ 2(0) + 4(0) + 2(0) - 5 = 0 $$
$$ -5 = 0 $$
The equation is not satisfied.
Therefore, the point P(0,0,0) from the first plane does not belong to the second plane.
The two planes cannot be coincident.
They are parallel planes.
Additional Notes
Further insights into parallel and inclined planes:
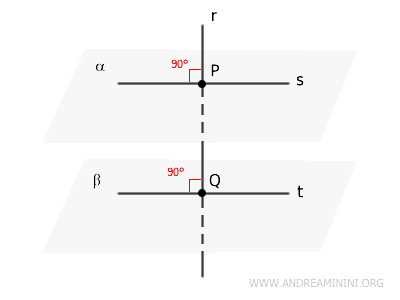
- Perpendicular Line to Two Planes Theorem
If two planes \( \alpha \) and \( \beta \) are both perpendicular to a line \( r \) at two distinct points \( P \) and \( Q \) on the line, then the planes must be parallel.
- Theorem of Parallel Planes Intersected by a Third Plane
When a plane \( \pi \) intersects two parallel planes \( \pi_1 \) and \( \pi_2 \), the intersections result in two parallel lines.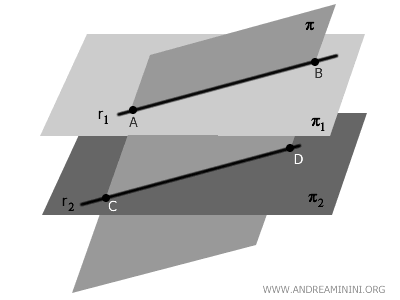
This happens because \( \pi_1 \) and \( \pi_2 \) are parallel and equidistant, meaning the plane \( \pi \) cuts through them to create two lines \( r_1 \) and \( r_2 \). Since \( \pi \) intersects both planes at the same angle, the lines \( r_1 \) and \( r_2 \) are necessarily parallel.
And so on.
