Plane Equation for Three Non-Collinear Points
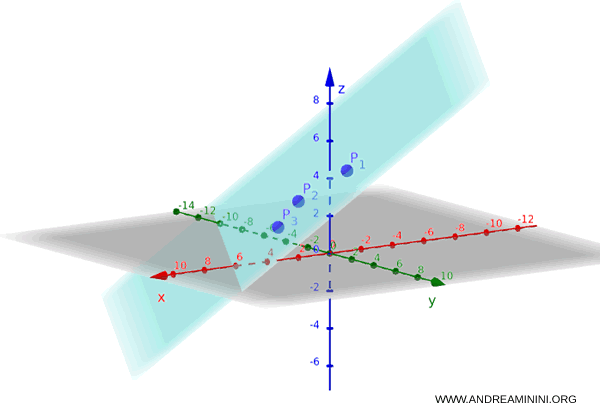
Given three non-collinear points in R3 space, there is a unique plane that passes through these points: P1, P2, and P3. $$ P_1 \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} $$
How to Determine the Parametric Equations of a Plane
Given three points $ P_1(x_1,y_1,z_1) $, $ P_2(x_2,y_2,z_2) $, and $ P_3(x_3,y_3,z_3) $, if the plane is not parallel to the z-axis, you can express it in explicit form as:
$$ z = mx + ny + q $$
By substituting the coordinates of the three points, you obtain a system of three equations:
$$ \begin{cases} mx_1 + ny_1 + q = z_1 \\ mx_2 + ny_2 + q = z_2 \\ mx_3 + ny_3 + q = z_3 \end{cases} $$
Solving this system yields the values of $ m $, $ n $, and $ q $, which define the equation of the plane.
Note. This method is valid only if the plane admits an explicit form - meaning it is not vertical (parallel to the $ z $-axis).
How can you tell if the system is solvable?
To check whether the system can be solved - that is, whether the three points define a plane that can be written as $ z = mx + ny + q $ - you can rewrite the system in matrix form:
$$
\begin{bmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
m \\
n \\
q
\end{bmatrix}
=
\begin{bmatrix}
z_1 \\
z_2 \\
z_3
\end{bmatrix}
$$
Here, $ A $ is the coefficient matrix:
$$
A =
\begin{bmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{bmatrix}
$$
The system has a unique solution if the determinant of $ A $ is nonzero:
$\det(A) \ne 0$
If $ \det(A) \ne 0 $, the plane is not parallel to the $ z $-axis, and the system can be solved to express the plane in explicit form.
If instead $ \det(A) = 0 $, the plane is vertical and cannot be expressed explicitly; however, you can still determine its implicit form, $ ax + by + cz + d = 0 $, using a different method.
What does $ \det(A) = 0 $ mean geometrically? If the determinant is zero, it means the projections of the three points onto the $ xy $-plane are collinear - in other words, the projected points $ (x_i,y_i) $ lie on a straight line. In this case, the plane is considered "vertical" and cannot be written in the form $ z = mx + ny + q $.
Example
Consider three non-collinear points in space:
$$ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $$
We can set up the following system of equations based on their coordinates:
$$ \begin{cases} mx_1 + ny_1 + q = z_1 \\ mx_2 + ny_2 + q = z_2 \\ mx_3 + ny_3 + q = z_3 \end{cases} $$
$$ \begin{cases} m(1) + n(3) + q = 5 \\ m(2) + n(0) + q = 3 \\ m(4) + n(1) + q =2 \end{cases} $$
$$ \begin{cases} m + 3n + q = 5 \\ 2m + q = 3 \\ 4m + n + q =2 \end{cases} $$
The coefficient matrix $ A $ is:
$$
A =
\begin{bmatrix}
1 & 3 & 1 \\
2 & 0 & 1 \\
4 & 1 & 1
\end{bmatrix}
$$
Next, we compute the determinant:
$$ \Delta = (1 \cdot 0 \cdot 1)+( 3 \cdot 1 \cdot 4) + (1 \cdot 2 \cdot 1) - (1 \cdot 0 \cdot 4) - (3 \cdot 2 \cdot 1) - (1 \cdot 1 \cdot 1) $$
$$ \Delta = 0+12+ 2 -0 -6- 1 = 7 $$
Since $ \Delta = 7 \ne 0 $, the system has a unique solution.
$$ \begin{cases} m + 3n + q = 5 \\ 2m + q = 3 \\ 4m + n + q =2 \end{cases} $$
We’ll solve the system using Cramer’s Rule.
First, we replace the first column with the constants $ (5,3,2) $:
$$ \Delta_m = \begin{vmatrix} 5 & 3 & 1 \\ 3 & 0 & 1 \\ 2 & 1 & 1 \end{vmatrix} $$
$$ \Delta_m = 5 \cdot \begin{vmatrix} 0 & 1 \\ 1 & 1 \end{vmatrix} - 3 \cdot \begin{vmatrix} 3 & 1 \\ 2 & 1 \end{vmatrix}
+ 1 \cdot \begin{vmatrix} 3 & 0 \\ 2 & 1 \end{vmatrix} $$
$$ \Delta_m = 5(-1) - 3(1) + 1(3) = -5 - 3 + 3 $$
$$ \Delta_m = -5 $$
Next, replace the second column:
$$ \Delta_n = \begin{vmatrix} 1 & 5 & 1 \\ 2 & 3 & 1 \\ 4 & 2 & 1 \end{vmatrix} $$
$$ \Delta_n = 1 \cdot \begin{vmatrix} 3 & 1 \\ 2 & 1 \end{vmatrix} - 5 \cdot \begin{vmatrix} 2 & 1 \\ 4 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 2 & 3 \\ 4 & 2 \end{vmatrix} $$
$$ \Delta_n = 1(1) - 5(-2) + 1(-8) = 1 + 10 - 8 $$
$$ \Delta_n = 3 $$
Finally, replace the third column:
$$ \Delta_q = \begin{vmatrix} 1 & 3 & 5 \\ 2 & 0 & 3 \\ 4 & 1 & 2 \end{vmatrix} $$
$$ \Delta_q = 1 \cdot \begin{vmatrix} 0 & 3 \\ 1 & 2 \end{vmatrix} - 3 \cdot \begin{vmatrix} 2 & 3 \\ 4 & 2 \end{vmatrix} + 5 \cdot \begin{vmatrix} 2 & 0 \\ 4 & 1 \end{vmatrix} $$
$$ \Delta_q = 1(-3) - 3(-8) + 5(2) = -3 + 24 + 10 $$
$$ \Delta_q = 31 $$
Now applying Cramer’s Rule:
$$ m = \frac{\Delta_m}{\Delta} = \frac{-5}{7} $$
$$ n = \frac{\Delta_n}{\Delta} = \frac{3}{7} $$
$$ q = \frac{\Delta_q}{\Delta} = \frac{31}{7} $$
Thus, the final result is:
$$ \begin{cases} m = -\frac{5}{7} \\ n = \frac{3}{7} \\ q = \frac{31}{7} \end{cases} $$
Substituting $ m $, $ n $, and $ q $ into the explicit equation of the plane $ z = mx + ny + q $, we obtain:
$$ -\frac{5}{7} x + \frac{3}{7}y + \frac{31}{7} = z $$
This is the equation of the plane passing through the points $ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $
An Alternative and More General Method
This alternative approach allows you to find the general (implicit) equation of a plane given three points:
$a x + b y + c z + d = 0$
The main advantage of this method is that it always works - whether the plane is vertical, horizontal, or oblique - and does not require solving a system of equations.
The trade-off is that it is a bit more advanced, as it relies on basic concepts from vector calculus.
How does it work?
You start with the coordinates of three points in space:
$$
P_1(x_1,y_1,z_1), \quad
P_2(x_2,y_2,z_2), \quad
P_3(x_3,y_3,z_3)
$$
From these, you construct two direction vectors that lie on the plane:
$$ \vec{v_1} = P_2 - P_1 = (x_2 - x_1, \ y_2 - y_1, \ z_2 - z_1) $$
$$ \vec{v_2} = P_3 - P_1 = (x_3 - x_1, \ y_3 - y_1, \ z_3 - z_1) $$
You then compute the cross product $ \vec{n} = \vec{v_1} \times \vec{v_2} $, which gives a normal vector to the plane:
$$
\vec{n} = (a, b, c) =
\left|
\begin{matrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
x_2 - x_1 & y_2 - y_1 & z_2 - z_1 \\
x_3 - x_1 & y_3 - y_1 & z_3 - z_1
\end{matrix}
\right|
$$
The components of this normal vector are exactly the coefficients $ a $, $ b $, and $ c $ in the general equation of the plane.
Alternatively, you can compute these coefficients directly using the following formulas:
$$ a = (y_2 - y_1)(z_3 - z_1) - (y_3 - y_1)(z_2 - z_1) $$
$$ b = (z_2 - z_1)(x_3 - x_1) - (z_3 - z_1)(x_2 - x_1) $$
$$ c = (x_2 - x_1)(y_3 - y_1) - (x_3 - x_1)(y_2 - y_1) $$
Once you have $ a $, $ b $, and $ c $, you can write the general form of the plane’s equation using any of the three given points:
$$ a (x - x_1) + b (y - y_1) + c (z - z_1) = 0 $$
Or, equivalently, you can expand this to the fully implicit form:
$$ a x + b y + c z + d = 0 $$
where the constant $ d $ is computed as:
$$ d = - (a x_1 + b y_1 + c z_1) $$
Both forms give you the general equation of the plane.
Moreover, if $ c \ne 0 $, you can solve for $ z $ to express the equation in explicit form:
$$ z = - \frac{a}{c} x - \frac{b}{c} y - \frac{d}{c} $$
Of course, this is only possible when $ c \ne 0 $. If $ c = 0 $, the plane is vertical with respect to the $ z $-axis, and the explicit form is not applicable.
Example
Let’s revisit the same three points used in the previous example:
$$
P_1 = (1, 3, 5), \quad
P_2 = (2, 0, 3), \quad
P_3 = (4, 1, 2)
$$
First, compute the plane’s direction vectors:
$$ \vec{v_1} = P_2 - P_1 = (2 - 1, \ 0 - 3, \ 3 - 5) = (1, \ -3, \ -2) $$
$$ \vec{v_2} = P_3 - P_1 = (4 - 1, \ 1 - 3, \ 2 - 5) = (3, \ -2, \ -3) $$
Next, compute the cross product of these two vectors:
$$ \vec{n} = \vec{v_1} \times \vec{v_2} = (a, b, c) $$
Using the determinant formula:
$$ \vec{n} = \left| \begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & -3 & -2 \\ 3 & -2 & -3 \end{matrix} \right| $$
$$ \vec{n} = \mathbf{i} \cdot \left| \begin{matrix}-3 & -2 \\ -2 & -3 \end{matrix} \right| - \mathbf{j} \cdot \left| \begin{matrix} 1 & -2 \\ 3 & -3 \end{matrix} \right| + \mathbf{k} \cdot \left| \begin{matrix} 1 & -3 \\ 3 & -2 \end{matrix} \right| $$
$$ \vec{n} = \mathbf{i} \cdot (9 - 4) - \mathbf{j} \cdot (-3 + 6) + \mathbf{k} \cdot (-2 - (-9)) $$
$$ \vec{n} = \mathbf{i} \cdot 5 - \mathbf{j} \cdot (-3) + \mathbf{k} \cdot 7 $$
$$ \vec{n} = 5 \mathbf{i} + 3 \mathbf{j} + 7 \mathbf{k} $$
Thus, the normal vector is $ \vec{n} = (5, 3, 7) $.
The corresponding coefficients are:
$$ a = 5, \quad b = 3, \quad c = 7 $$
We can now write the plane’s equation:
$$ 5(x - 1) - 3(y - 3) + 7(z - 5) = 0 $$
Expanding the terms:
$$ 5x - 5 - 3y + 9 + 7z - 35 = 0 $$
$$ 5x - 3y + 7z - (5 - 9 + 35) = 0 $$
$$ 5x - 3y + 7z - 31 = 0 $$
Thus, the general equation of the plane is:
$$ 5x - 3y + 7z = 31 $$
Since the coefficient of $ z $ is nonzero, we can also rewrite the plane’s equation in explicit form:
First, solve for $ z $:
$$ 7z = -5x + 3y + 31 $$
Then divide through by 7:
$$ z = -\frac{5}{7} x + \frac{3}{7} y + \frac{31}{7} $$
This is the explicit equation of the plane passing through the three given points - exactly the same result we obtained with the previous method.
Vector Method
From the three points, we derive two direction vectors:
$$ v_1 = P_1P_2 = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} - \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} $$
$$ v_2 = P_1P_3 = \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} - \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$
Next, we check that they are linearly independent.
The two vectors can generate the plane, forming a basis of the vector space, only if they are linearly independent.
Two vectors are linearly independent if the rank of the matrix formed by placing the vectors in columns is equal to the number of vectors.
$$ r_k \begin{pmatrix} x_2 - x_1 & x_3 - x_1 \\ y_2 - y_1 & y_3 - y_1 \\ z_2 - z_1 & z_3 - z_1 \end{pmatrix} = 2 $$
Once the linear independence of the two vectors is confirmed, we choose one of the three points as an arbitrary point P0 on the plane.
For example, we choose the point P1.
$$ P_0 = P_1 $$
$$ \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} $$
Now we have all the elements to write the vector equation of the plane.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \cdot v_1 + t_2 \cdot v_2 $$
Where t1 and t2 are parameters of the vector equation that determine all points on the plane.
We substitute the two direction vectors:
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$
Then substitute the point P0:
Thus, we obtain the vector equation of the plane:
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$
To find the parametric equation of the plane, we convert the vector form into a system of three equations:
$$ \begin{cases} x = x_0 + t_1 \cdot ( x_2 - x_1 ) + t_2 \cdot ( x_3 - x_1 ) \\ y = y_0 + t_1 \cdot ( y_2 - y_1 ) + t_2 \cdot ( y_3 - y_1 ) \\ z = z_0 + t_1 \cdot ( z_2 - z_1 ) + t_2 \cdot ( z_3 - z_1 ) \end{cases} $$
To find the Cartesian equation, we solve the parametric equations:
Move the point P0 to the left side:
$$ \begin{cases} x - x_0 = t_1 \cdot ( x_2 - x_1 ) + t_2 \cdot ( x_3 - x_1 ) \\ y - y_0 = t_1 \cdot ( y_2 - y_1 ) + t_2 \cdot ( y_3 - y_1 ) \\ z - z_0 = t_1 \cdot ( z_2 - z_1 ) + t_2 \cdot ( z_3 - z_1 ) \end{cases} $$
Next, construct the matrix with the coefficients of the three vectors as columns:
$$ \begin{pmatrix} x-x_0 & x_2 - x_1 & x_3 - x_1 \\ y-y_0 & y_2 - y_1 & y_3 - y_1 \\ z-z_0 & z_2 - z_1 & z_3 - z_1 \end{pmatrix} $$
Finally, calculate the determinant of the matrix and set it equal to zero:
$$ det \begin{pmatrix} x-x_0 & x_2 - x_1 & x_3 - x_1 \\ y-y_0 & y_2 - y_1 & y_3 - y_1 \\ z-z_0 & z_2 - z_1 & z_3 - z_1 \end{pmatrix} = 0 $$
$$ ( x-x_0 ) \cdot \begin{vmatrix} y_2-y_1 & y_3 - y_1 \\ z_2 - z_1 & z_3 - z_1 \end{vmatrix} - (y-y_0) \cdot \begin{vmatrix} x_2-x_1 & x_3 - x_1 \\ z_2 - z_1 & z_3 - z_1 \end{vmatrix} +(z-z_0) \cdot \begin{vmatrix} x_2-x_1 & x_3 - x_1 \\ y_2-y_1 & y_3 - y_1 \end{vmatrix} = 0$$
We thus obtain the Cartesian equation of the plane:
$$ ( x-x_0 ) \cdot a - (y-y_0) \cdot b +(z-z_0) \cdot c = 0$$
Example
Let's consider three non-collinear points in space:
$$ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $$
From these points, we derive the direction vectors:
$$ v_1 = P_1P_2 = \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} - \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} = \begin{pmatrix} 2 - 1 \\ 0 - 3 \\ 3 - 5 \end{pmatrix} = \begin{pmatrix} 1 \\ -3 \\ -2 \end{pmatrix} $$
$$ v_2 = P_1P_3 = \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} - \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} = \begin{pmatrix} 4 - 1 \\ 1 - 3 \\ 2 - 5 \end{pmatrix} = \begin{pmatrix} 3 \\ -2 \\ -3 \end{pmatrix} $$
We check that they are linearly independent:
$$ r_k \begin{pmatrix} 1 & 3 \\ -3 & -2 \\ -2 & -3 \end{pmatrix} = 2 $$
The rank (rk=2) equals the number of vectors (2).
Thus, the vectors are linearly independent and can be used as the basis vectors for the plane.
We choose point P1 as an arbitrary point P0 on the plane:
$$ P_0 = P_1 $$
$$ \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} = \begin{pmatrix}1 \\ 3 \\ 5 \end{pmatrix} $$
Now we have all the elements to write the vector equation of the plane:
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \cdot v_1 + t_2 \cdot v_2 $$
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix}1 \\ 3 \\ 5 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 1 \\ -3 \\ -2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 3 \\ -2 \\ -3 \end{pmatrix} $$
From this, we obtain the parametric equation of the plane:
$$ \begin{cases} x = 1 + t_1 \cdot 1 + t_2 \cdot 3 \\ y = 3 + t_1 \cdot (-3) + t_2 \cdot (-2) \\ z = 5 + t_1 \cdot (-2) + t_2 \cdot (-3) \end{cases} $$
$$ \begin{cases} x = 1 + t_1 + 3 t_2 \\ y = 3 - 3 t_1 -2 t_2 \\ z = 5 - 2 t_1 -3 t_2 \end{cases} $$
Finally, we derive the Cartesian equation of the plane by calculating the determinant of the matrix:
Move the coordinates of point P0 to the left side:
$$ \begin{cases} x - 1 = t_1 + 3 t_2 \\ y - 3 = - 3 t_1 -2 t_2 \\ z - 5 = - 2 t_1 -3 t_2 \end{cases} $$
Transform the system into a matrix:
$$ \begin{pmatrix} x - 1 & 1 & 3 \\ y-3 & -3 & -2 \\ z-5 & -2 & -3 \end{pmatrix} $$
Calculate the determinant of the matrix:
$$ det \begin{pmatrix} x - 1 & 1 & 3 \\ y-3 & -3 & -2 \\ z-5 & -2 & -3 \end{pmatrix} $$
$$ ( x-1 ) \cdot \begin{vmatrix} -3 & -2 \\ -2 & -3 \end{vmatrix} - (y-3) \cdot \begin{vmatrix} 1 & 3 \\ -2 & -3 \end{vmatrix} +(z-5) \cdot \begin{vmatrix} 1 & 3 \\ -3 & -2 \end{vmatrix} $$
$$ ( x-1 ) \cdot (5) - (y-3) \cdot (3) +(z-5) \cdot (7) $$
$$ 5x - 5 -3y +9 +7z -35 $$
$$ 5x -3y +7z -31 $$
Set the equation to zero to get the Cartesian equation of the plane:
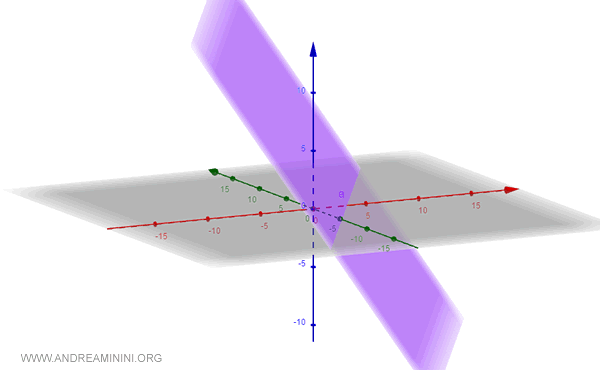
$$ 5x -3y +7z -31 = 0 $$
The graphical representation of the plane in three-dimensional space is shown below:
And so on.
