Determinant of a matrix

In linear algebra, the determinant of a square matrix is a scalar value that reveals key properties of the matrix. Denoted by det(A) or |A|, it encapsulates both the algebraic and geometric characteristics of the matrix.

Example

For a square matrix

$$ A= \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$

its determinant is denoted by det(A):

$$ det(A) = -2 $$

or alternatively, using two vertical bars:

$$ | A | = \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = -2 $$

Note. The determinant can only be computed for square matrices, i.e., matrices with an equal number of rows and columns (m=n).

Finding the Determinant of a Matrix

Square Matrices of Order 1

For a 1x1 matrix, which contains a single element, the determinant is simply the value of that element, a₁₁.

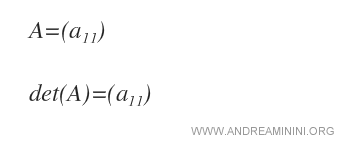
Example. A matrix A of order 1 has one element, a₁₁ = 5. Thus, det(A) = 5.

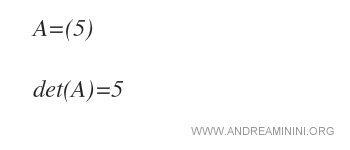
Square Matrices of Order 2

For a 2x2 matrix, the determinant is calculated by taking the product of the elements on the main diagonal (a₁₁·a₂₂) and subtracting the product of the elements on the secondary diagonal (a₂₁·a₁₂).

Example. For the following 2x2 matrix A, which has two rows and two columns, det(A) = -2.

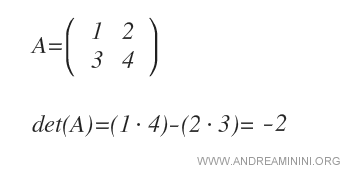
Sarrus' Rule

Sarrus' rule applies to 3x3 matrices (m=n=3) to find their determinant.

Consider a 3x3 matrix:

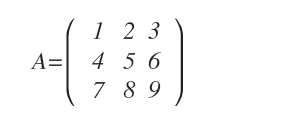
Place the first two columns to the right:

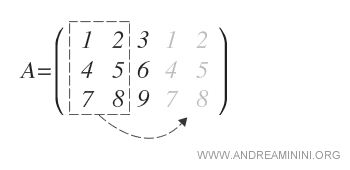
Then, add the products of the diagonals from the top left to the bottom right:

Next, subtract the products of the diagonals from the bottom left to the top right.

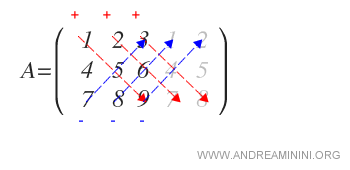
The resulting algebraic sum of these products is the determinant of the matrix.

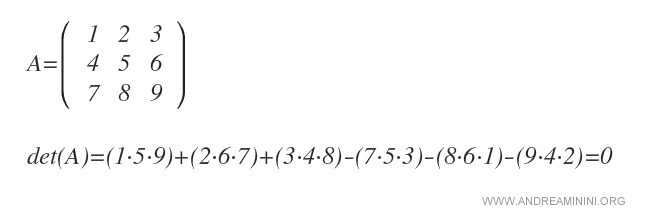
The Sarrus rule summarized

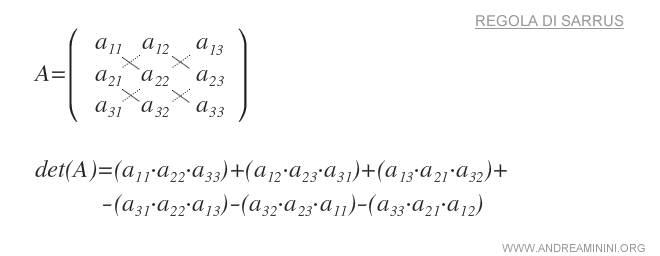
Laplace's Method

Laplace's method is one of the most widely used techniques for calculating determinants. It systematically reduces a determinant of order n to smaller determinants of order n-1.

Named after Pierre-Simon Laplace, this method is explained as follows:

How it works

Laplace’s method transforms the determinant calculation into smaller sub-determinants.

1. Choose any column j of the matrix.

   Which column is best to choose? Any column will work, but selecting one with more zeros often reduces the number of steps.

2. Once column j is chosen, compute the determinants of the submatrices A(ij) by eliminating row i and column j from matrix A, using the following formula.
   

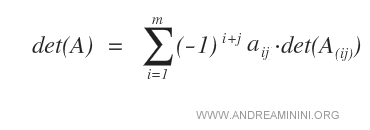
Example. To find the determinant of a 3x3 matrix A, I use the Laplace expansion along column j=1. Summing the submatrix determinants results in det(A) = 0.

Row Laplace Method

Alternatively, the Laplace method can also be applied by selecting a row instead of a column.

In this case, the formula varies slightly as columns j are cycled from 1 to n.

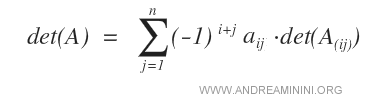
This produces the same result.

Example. Here, I select the first row: $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot \begin{vmatrix} 1 & 2 & 3 \\ 0 & 5 & 1 \\ 0 & 0 & 2 \end{vmatrix} - 3 \cdot \begin{vmatrix} 0 & 2 & 3 \\ 0 & 5 & 1 \\ 0 & 0 & 2 \end{vmatrix} + 5 \cdot \begin{vmatrix} 0 & 1 & 3 \\ 0 & 0 & 1 \\ 0 & 0 & 2 \end{vmatrix} - 1 \cdot \begin{vmatrix} 0 & 1 & 2 \\ 0 & 0 & 5 \\ 0 & 0 & 0 \end{vmatrix} $$ Calculating the four submatrix determinants: $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot 10 - 3 \cdot 0 + 5 \cdot 0 - 1 \cdot 0 $$ The determinants of the submatrices are then multiplied by their coefficients and summed. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 20 $$ The matrix determinant is 20.

A Tip to Simplify Calculations. When using this method, choosing the row or column with the most zeros simplifies the calculation. In this case, I select the fourth row. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = - 0 \cdot A_{(4,1)} + 0 \cdot A_{(4,2)} - 0 \cdot A_{(4,3)} + 2 \cdot \begin{vmatrix} 2 & 3 & 5 \\ 0 & 1 & 2 \\ 0 & 0 & 5 \end{vmatrix} $$ Since many coefficients are zero, I avoid calculating three determinants. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot \begin{vmatrix} 2 & 3 & 5 \\ 0 & 1 & 2 \\ 0 & 0 & 5 \end{vmatrix} $$ Then, I repeat the process for the third row of the submatrix. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot 5 \cdot \begin{vmatrix} 2 & 3 \\ 0 & 1 \end{vmatrix} = 2 \cdot 5 \cdot (2 \cdot 1) = 20 $$ This reduces a 4x4 matrix determinant to a 2x2. However, as this matrix is triangular, we could also find the determinant by multiplying the main diagonal elements. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot 1 \cdot 5 \cdot 2 = 20 $$

Limitations of Laplace's Method. Using Laplace’s method for large matrices is inefficient. For high-order square matrices, methods like Gaussian elimination are far more efficient.

Gaussian Elimination Method

The Gaussian elimination method can also be used to find a matrix’s determinant.

Using Gaussian transformations, I convert the matrix into an upper triangular form.

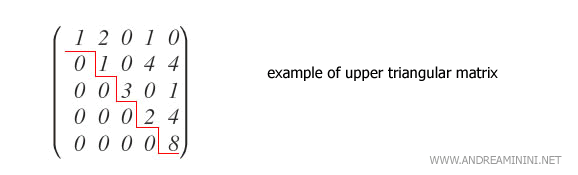
In triangular matrices, the determinant is simply the product of the main diagonal elements, making the calculation straightforward.

However, I must account for any sign changes.

Swapping two rows (Rx⇔Ry) reverses the determinant’s sign (-1·det).

Multiplying a row by a scalar (k Rx) scales the determinant by that factor (k det).

Adding a row to a multiple of another row (Rx+k·Ry) does not affect the determinant’s sign.

Example. In this exercise, I use Gaussian elimination to calculate the determinant of matrix A.

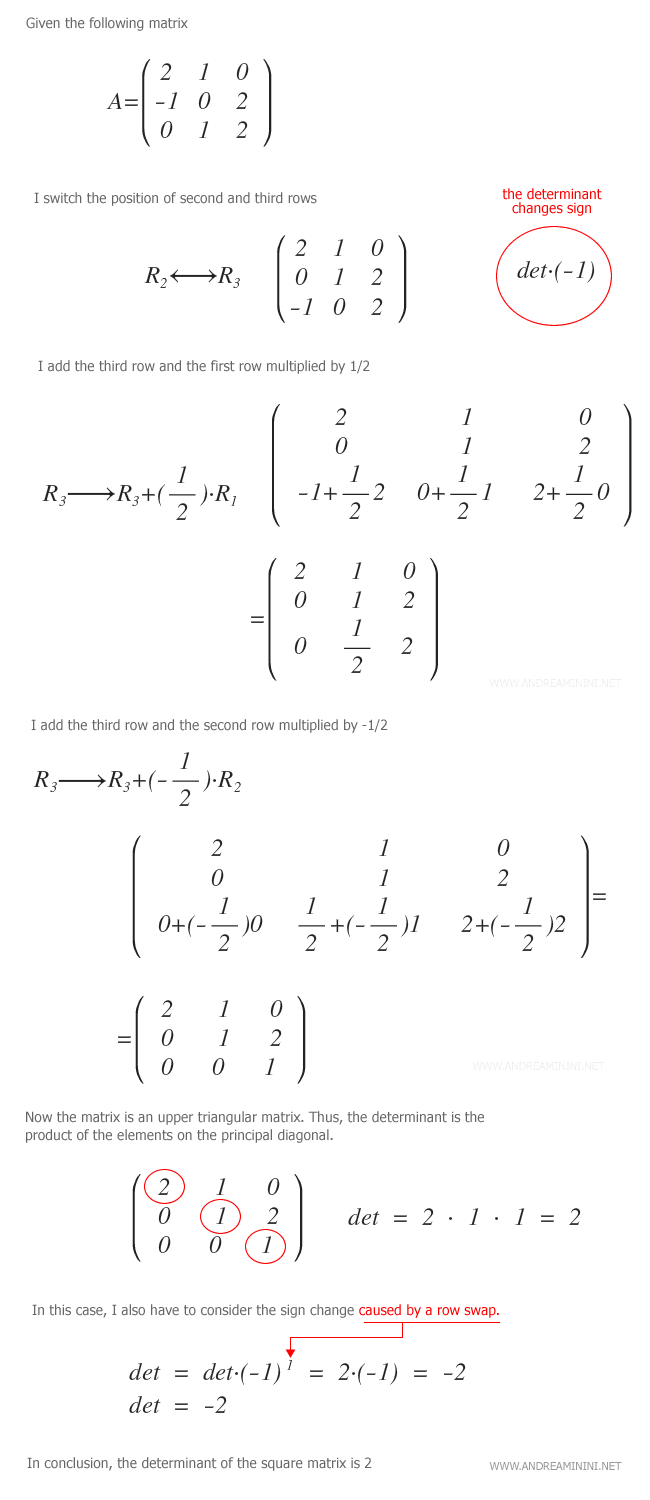
Advantages of the Gaussian Method

For large matrices, Gaussian elimination is much faster than Laplace expansion.

Determinant Properties

Key properties of the determinant of square matrices:

• If a square matrix has at least one row or column made up entirely of zeros, its determinant is zero.

  Example. $$ \begin{vmatrix} 1 & 2 & 3 \\ 0 & 0 & 0 \\ 7 & 8 & 9 \end{vmatrix} = 0 $$ $$ \begin{vmatrix} 1 & 2 & 0 \\ 4 & 5 & 0 \\ 7 & 8 & 0 \end{vmatrix} = 0 $$

• If a square matrix is diagonal, upper triangular, or lower triangular, its determinant is the product of the elements along the main diagonal.

  Example. $$ \begin{vmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 0 & 0 & 9 \end{vmatrix} = 1 \begin{vmatrix} 5 & 6 \\ 0 & 9 \end{vmatrix} - 2 \begin{vmatrix} 0 & 6 \\ 0 & 9 \end{vmatrix} + 3 \begin{vmatrix} 0 & 5 \\ 0 & 0 \end{vmatrix} $$ $$ = 1 \cdot (5 \cdot 9 - 6 \cdot 0) - 2 \cdot (0 \cdot 9 - 6 \cdot 0) + 3 \cdot (0 \cdot 0 - 5 \cdot 0) $$ $$ = 1 \cdot 5 \cdot 9 $$

• The determinant of a matrix \( A \) is equal to the determinant of its transpose \( A^T \): $$ det(A) = det(A^T) $$

  Example. $$ det(A) = \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = -2 $$ $$ det(A^T) = \begin{vmatrix} 1 & 3 \\ 2 & 4 \end{vmatrix} = -2 $$

• If a square matrix has two identical rows or two identical columns, its determinant is zero.

  Example. If a matrix has two identical rows: $$ det(A) = \begin{vmatrix} a & b \\ a & b \end{vmatrix} = ab - ba = 0 $$ $$ det(A) = \begin{vmatrix} a & b & c \\ a & b & c \\ d & e & f \end{vmatrix} = d \begin{vmatrix} b & c \\ b & c \end{vmatrix} - e \begin{vmatrix} a & c \\ a & c \end{vmatrix} + f \begin{vmatrix} a & b \\ a & b \end{vmatrix} = d \cdot 0 - e \cdot 0 + f \cdot 0 = 0 $$ If a matrix has two identical columns, its transpose will have two identical rows, which means the determinant must be zero as well. $$ det(A) = \begin{vmatrix} a & a \\ b & b \end{vmatrix} = det(A^T) = \begin{vmatrix} a & b \\ a & b \end{vmatrix} = 0 $$

• Swapping two rows (or two columns) in a square matrix results in the determinant changing sign.

  Example. The determinant of this matrix is -2: $$ \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = -2 $$ Swapping the two rows gives: $$ \begin{vmatrix} 3 & 4 \\ 1 & 2 \end{vmatrix} = 2 $$ The determinant is now the negative of the original value.

• Binet's Theorem
  For two square matrices \( A \) and \( B \) of order \( n \), the determinant of their product equals the product of their determinants: $$ det(A \cdot B) = det(A) \cdot det(B) $$

  Example. Consider the matrices: $$ A=\begin{pmatrix} 1 & 4 \\ 3 & 2 \end{pmatrix} $$ $$ B=\begin{pmatrix} 2 & 1 \\ 5 & 3 \end{pmatrix} $$ Their determinants are: $$ det(A) = -10 $$ $$ det(B) = 1 $$ Computing their product: $$ A \cdot B =\begin{pmatrix} 1 & 4 \\ 3 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\ 5 & 3 \end{pmatrix} = \begin{pmatrix} 22 & 13 \\ 16 & 9 \end{pmatrix} $$ The determinant of the resulting matrix is: $$ \det(A \cdot B) = -10 $$ Multiplying the determinants of \( A \) and \( B \) confirms the theorem: $$ \det(A) \cdot \det(B) = -10 \cdot 1 = -10 $$

• For any square matrix \( M \) of order \( n \) and a scalar \( k \), the following holds: $$ \det(k \cdot M) = k^n \cdot \det(M) $$

  Proof. Scaling a \( 2 \times 2 \) matrix by a scalar \( k \) gives: $$ k \cdot M = \begin{pmatrix} ka & kb \\ kc & kd \end{pmatrix} $$ The determinant is then: $$ det(k \cdot M) = ka \cdot kd - kb \cdot kc = k^2ad-k^2bc =k^2 \cdot (ad-bc)=k^2 \cdot det(M) $$ This property is especially useful for simplifying a matrix when all elements share a common factor.
  Example. In this matrix, all elements are divisible by 2: $$ M = \begin{pmatrix} 6 & 8 \\ 4 & 2 \end{pmatrix} $$ To compute its determinant, factor out 2 and adjust accordingly: $$ \det(M) = 2^2 \cdot det \begin{pmatrix} \frac{6}{2} & \frac{8}{2} \\ \frac{4}{2} & \frac{2}{2} \end{pmatrix} = 4 \cdot det \begin{pmatrix} 3 & 4 \\ 2 & 1 \end{pmatrix} = 4 \cdot (3 \cdot 1 - 4 \cdot 2) = -20 $$ Working with smaller numbers makes the calculation easier.

• If a square matrix \( M \) has a row or column that is a multiple of another, its determinant is zero.

  Example. This matrix has a row that is a multiple of another: $$ det \begin{pmatrix} 2 & 4 \\ 4 & 8 \end{pmatrix} = 2 \cdot 8 - 4 \cdot 4 = 16 - 16 = 0 $$ The determinant is zero.

Determinant of Triangular Matrices

The determinant of a triangular matrix is simply the product of the elements along its main diagonal.

This happens because all other terms in the determinant expansion are zero.

As a result, finding the determinant of a triangular matrix is straightforward and requires minimal computation.

Example

Consider the following matrix:

$$ A = \begin{pmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{pmatrix} $$

Since \( A \) is triangular, its determinant is simply the product of the entries on the main diagonal:

$$ det(A) = 2 \cdot 1 \cdot 5 \cdot 2 = 20 $$

Key Observations

Here are some important properties of the determinant:

• The determinant is a complete invariant under transposition, meaning that a square matrix \( M \) and its transpose \( M^T \) have the same determinant: $$ \det(M) = \det(M^T) $$

Online Determinant Calculator

Use this tool to quickly compute the determinant of any square matrix online.

And so on