Main diagonal of a square matrix

The main diagonal of a square matrix of order n consists of elements where the row and column indices are equal. In other words, $$ a_{11} , \ a_{22} , \ a_{33} , \ ... , \ a_{nn} . $$

This diagonal stretches from the top-left corner of the matrix to the bottom-right corner.

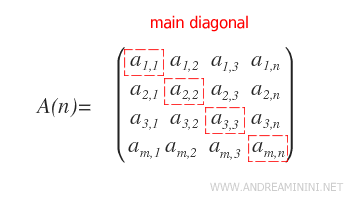
Note: The main diagonal applies only to square matrices, which have the same number of rows and columns.

Example

Consider a square matrix of order n=3, which means it has three rows and three columns.

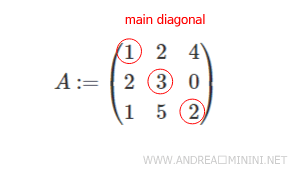
This illustration shows the main diagonal in a 3x3 matrix.

The elements on the main diagonal are as follows:

$$ a_{11} = 1 $$

$$ a_{22} = 3 $$

$$ a_{33} = 2 $$

and so forth.