Scalar Matrix

A scalar matrix is a square matrix where each entry on the main diagonal holds the same constant value (other than zero), while all off-diagonal elements are zero.

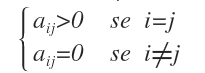
In other words, it’s a specific type of diagonal matrix with identical values along the main diagonal.

Example: The matrix below is an example of a scalar matrix.

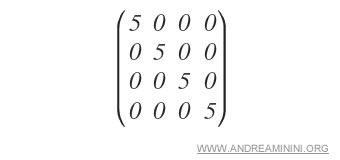
A scalar matrix is formed by multiplying the identity matrix by a constant.

This type of matrix can always be expressed as a multiple of the identity matrix.

Given a scalar value α, a scalar matrix is simply the product of α and the identity matrix I.

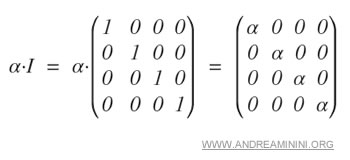
Properties of Scalar Matrices

Scalar matrices exhibit a unique property: they retain the commutative property under matrix multiplication.

For any real number α, scalar matrix I(n), and matrix A, the product α·I(n)·A equals α·A·I(m), resulting in the scalar product α·A in both cases.

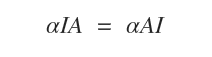
Example: A practical application of scalar matrices.