Similar Matrices

In the domain of matrices of order n, two matrices A and B are called similar matrices if there exists an invertible matrix M such that:

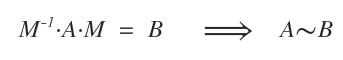
In this case, the similarity between the two matrices is denoted by the similarity operator ∼ (tilde).

Similarity is an equivalence relation in the set of all matrices of order n.

Properties of Similar Matrices

1. Each matrix is similar to itself.
2. If matrix A is similar to matrix B, then matrix B is similar to matrix A.
3. If matrix A is similar to matrix B and matrix B is similar to matrix C, then matrix A is similar to matrix C.
4. Similar matrices share the same eigenvalues and possess the same determinant, rank, and trace.
5. Similar matrices can be described as an endomorphism with respect to different bases B1 and B2 of a vector space V.
6. Similar matrices have the same characteristic polynomial.

A Practical Example of Similar Matrices

Consider these two matrices A and B

$$ A = \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix} $$

$$ B = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

They are similar because there exists an invertible matrix M

$$ M = \begin{pmatrix} 1 & 1 & 1 \\ -2 & 1 & 0 \\ 1 & 1 & -1 \end{pmatrix} $$

$$ M^{-1} = \begin{pmatrix} 1/6 & -1/3 & 1/6 \\ 1/3 & 1/3 & 1/3 \\ 1/2 & 0 & -1/2 \end{pmatrix} $$

Such that

$$ M^{-1}AM = B $$

Indeed

$$ \begin{pmatrix} 1/6 & -1/3 & 1/6 \\ 1/3 & 1/3 & 1/3 \\ 1/2 & 0 & -1/2 \end{pmatrix} \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 \\ -2 & 1 & 0 \\ 1 & 1 & -1 \end{pmatrix} = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$