Bordered matrix theorem
The Bordered Theorem is a practical method for calculating the rank of matrices more quickly, bypassing the need to consider all minors of order k.
It's also known as the Bordering Method, the Orlando Theorem, or Kronecker's Theorem.
Definition
Let b be a non-zero minor of order k of a submatrix B of A.
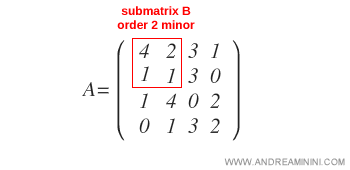
Note. The minor is the determinant of the submatrix B. $$ \Delta_B = 4 \cdot 1 - 2 \cdot 1 = 2 $$
If all minors of order k+1 obtained by bordering submatrix B are zero.
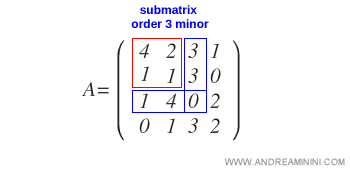
What does it mean to border a submatrix? It’s like adding a border to a blanket. This involves adding a row and a column to the submatrix of order k, chosen from the remaining parts of the matrix, to transform it into a submatrix of order k+1. For instance, the minors obtained by bordering submatrix B are called borders of B.
Thus, all minors of order k+1 of matrix A are null, and the rank of matrix A is equal to k.
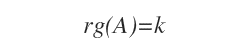
Note. There is more than one bordered submatrix. For example, submatrix B can be bordered by combining the remaining rows and columns of matrix A. There are 4 possible combinations and as many bordered submatrices whose minors need to be calculated.
A Practical Example
The following 4x4 matrix has a rank between 0 and 4.
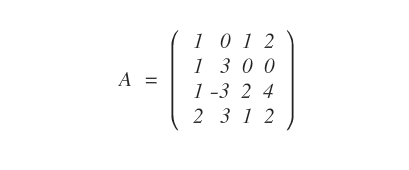
Since there is at least one non-zero element, the matrix's rank is between 1 and 4.
To check if the matrix has a rank of 2, I calculate the minor of any 2x2 submatrix.
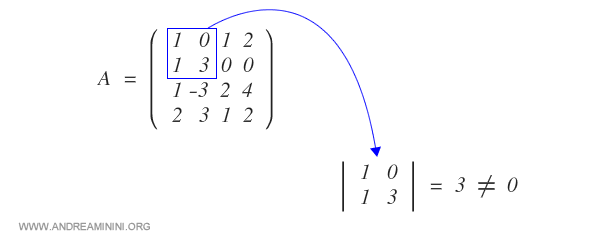
The order 2 minor taken as a reference is non-zero, so the rank of the matrix is between 2 and 4.
Now, I apply the Bordering Theorem to the previous submatrix to see if there's a rank 3 for the matrix.
The matrix can be "bordered" in four different ways:
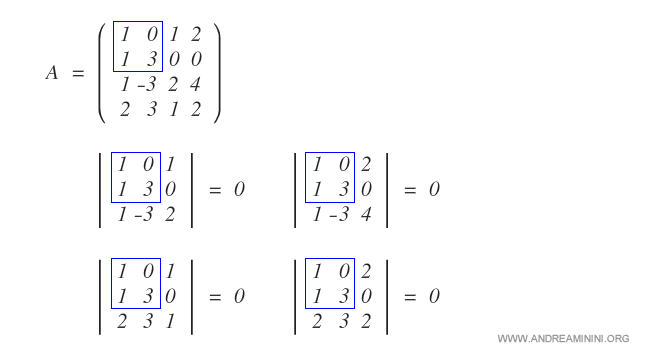
All minors of the bordered matrix are null.
According to the Bordering Theorem, matrix A does not have a rank equal to 3.
If there's no rank of order k=3, then there are no ranks of higher order k>3 either.
Therefore, the maximum rank of the matrix is k=2, and matrix A has a rank equal to rk(A)=2.
Useful Observations
Some useful observations about the Bordering Theorem
- A matrix has a rank rk(M)=0, which is zero only if it's a null matrix.
Proof. If the matrix is null (M=0), all its elements are zero, thus all its minors of order k=1 are null.
- The rank of matrix M is always equal to the rank of its transpose MT $$ rk(M) = rk(M^T) $$
Explanation. A square matrix has the same determinant as its transpose. Therefore, the rank of a matrix M is necessarily equal to that of its transpose MT.
- If a matrix M has a rank rk(M)=n then all its minors of order higher than n are null.
- If in a matrix M all minors of order n are null, then the rank of the matrix is less than n $$ rk(M)<n $$
And so on.
