Matrix rank

The rank of a matrix A is the largest order non-zero minor. It is also referred to as the characteristic of the matrix.

Given a matrix A of size mxn, its rank is p if there exists at least one minor of order p with a non-zero determinant, and all minors of order p+1, if they exist, have a determinant equal to zero.

The rank of matrix A is a real number and is denoted by the symbols rk(A), rg(A), r(A), or p(A).

Note. Put simply, the rank of a matrix is the maximum order of minors with non-zero determinants.

How to calculate the rank of a matrix

If matrix A belongs to M_mxn, then the rank of matrix A, denoted as r(A), is between zero and the smaller integer value of rows and columns.

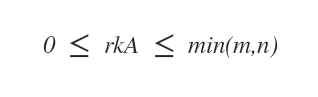
The rank of a matrix represents the maximum number of linearly independent rows or columns in the matrix.

Thus, the number of linearly independent rows or columns cannot exceed the number of rows or columns of the matrix, respectively.

Note. Note that by convention, only the zero matrix has rank zero. All other matrices have a rank greater than or equal to one.

A Practical Example

In this example, we will calculate the rank of a 3x4 matrix.

The rank of the matrix is equal to 3

Note. Note: When calculating the rank of a matrix, it is not necessary to verify all the minors of every order. Instead, we can simply find the first non-zero minor of order N and move on to the next order, N+1.

Maximum or Full Rank

When the rank=min(m,n), it is referred to as the maximum or full rank.

Practical Example

Here is a practical example of a matrix with full rank.

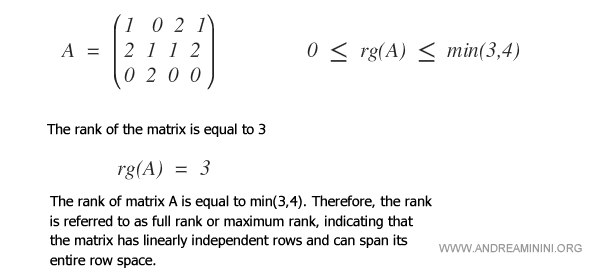
Note. In square matrices of order n, the rank can only coincide with the order of the matrix itself (i.e., rg(A)=n) if the determinant of the matrix is non-zero.

The properties of rank

The rank of matrices has the following properties:

1. The rank of a matrix A is equal to the rank of its transpose A^T.
   
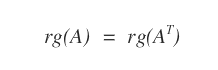
2. The rank is equal to zero only in null matrices.
3. If all minors of order N are null, then all higher orders of the matrix are also null.

   Proof. Suppose all minors of order k of a matrix are null, where k is less than the minimum value between the number of rows m and columns n (k<min{m,n}). Consider a minor of order j where k<j≤min{m,n}. In Laplace expansion, the determinant of a matrix of order j reduces to the calculation of determinants of square submatrices of order j-1. And so on until the calculation of determinants of square submatrices of order j-1=k. Since the minors of order k are null, it follows that all minors of order higher than k are also null.

Other methods for calculating the rank

There are different methods to calculate the rank of a matrix.

One common approach is to compute all the minors of the matrix, but this can be time-consuming.

To speed up the process, there are alternative methods available, such as Kronecker's theorem and Gaussian elimination.

Rank and the Visualization of Vectors in Linear Algebra

The rank of a matrix, comprising row or column vectors, serves as an indicator of the amount of independent information available for the spatial representation of vectors.

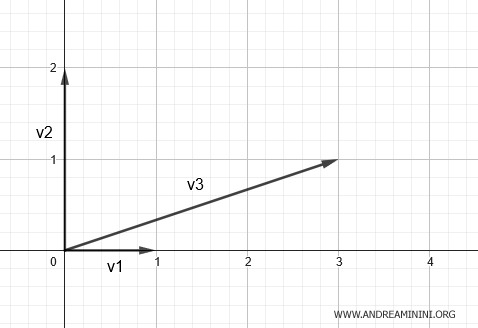
To illustrate, consider the 2x3 matrix:

$$ M_1 = \begin{pmatrix} 1 & 0 & 3 \\ 0 & 2 & 1 \end{pmatrix} $$

This matrix possesses a rank of 2.

$$ rk(M_1)= 2 $$

Interpreting this, the column vectors v1=(1;0), v2=(0;2), and v3=(3;1) can be depicted in two orthogonal directions, essentially spanning a plane.

For further clarity, let's delve into another example:

$$ M_2 = \begin{pmatrix} 2 & 4 & 6 \\ 1 & 2 & 3 \end{pmatrix} $$

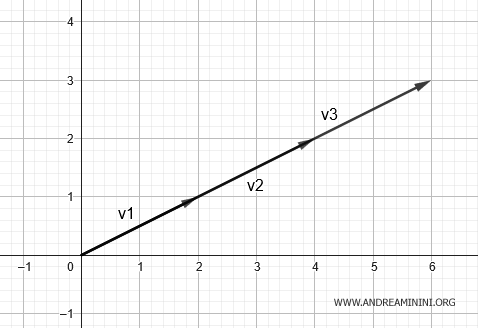
This matrix has a rank of 1, given that one row is a scalar multiple of the other, leading to redundant information.

$$ rk(M_2)= 1 $$

This suggests that the vectors v1=(2;1), v2=(4;2), and v3=(6;3) reside in a one-dimensional subspace, akin to a line.

In such cases, there's an absence of information along one of the plane's axes.

A Note on Higher Dimensions. It's worth mentioning that for an n-dimensional matrix where n exceeds 3, even if a graphical representation becomes infeasible, the rank remains a pivotal metric, shedding light on the extent of independent information at hand.

Observations

Here are some useful observations regarding the calculation of the rank of a matrix:

• Two matrices A and B are row-equivalent if and only if they have the same rank, which can be written as $$ rk(A) = rk(B) $$ This holds true for both square and rectangular matrices.
• The rank is an invariant property of matrix transposition, meaning that the rank of a square matrix M and its transpose MT always remain the same, which can be written as $$ rk(M) = rk(M^T) $$