Matrix Rank Using Gaussian Elimination

The rank of a matrix can be effectively determined through the process of Gaussian elimination.

Let A be an m x n matrix and B a row echelon form obtained from A via Gaussian elimination. Then, the rank of matrix A is equal to the number of pivot positions in matrix B.

A practical example

We aim to determine the rank of matrix A.

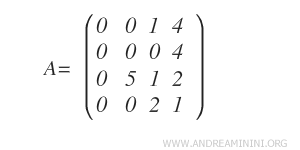
By applying Gaussian elimination, we can reduce matrix A to a row echelon form B.

Matrix B is row-equivalent to matrix A.

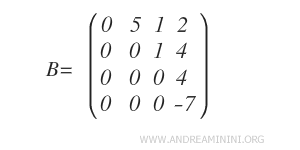
In this case, matrix B contains three pivot positions.

Note. A pivot is the first non-zero entry in a row, reading from left to right, with all entries directly below it equal to zero. Pivots are not required to be equal to one in this context.

Thus, we conclude that the rank of matrix A is 3.

This method allows us to compute the rank of matrix A without resorting to the calculation of minors.

It provides an efficient alternative approach to determining the rank of a matrix.