Matrices
An Introduction to Matrices
A matrix is an ordered table of elements ai,j, where ai,j are numbers called elements (or coefficients) and the indices i,j in subscript to the elements are positive integers that conventionally indicate the row number (i) first and then the column number (j).
If the elements of the matrix A are real numbers, the matrix A is called real coefficient matrix

A generic element (i,j) is found in the i-th row and j-th column.
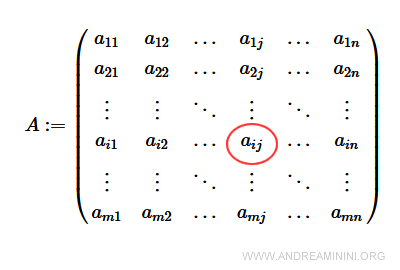
The indices of the elements can be indicated with a comma (am,n) or without a comma (amn) between the indices.
Note. The comma notation prevents ambiguity when the indices exceed ten.
Other concise notations used to denote matrices include A(m,n) , Amxn or A=(amn).
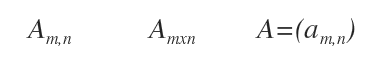
The total number of rows and columns (m x n) is referred to as the dimension of the matrix.
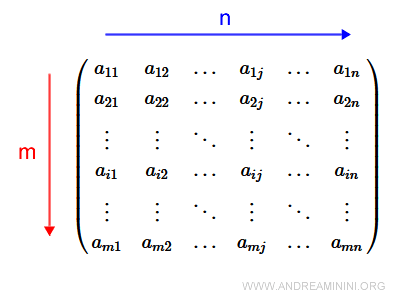
Therefore, m and n represent the dimensions of a generic matrix of type (m, n).
If the number of rows is equal to the number of columns (m = n), the matrix is called a square matrix.
What is the purpose of a matrix? Matrices are mathematical objects primarily used in linear algebra to represent and solve systems of m equations and n variables.
A Matrix Example
Here is an example of a matrix of type (2,3).
$$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$
The elements of the matrix are:$$ a_{11}=3 \\ a_{12} = 1 \\ a_{13} = 6 \\ a_{21}=0 \\ a_{22} = 4 \\ a_{23} = -1 $$
Where the elements a11, a12 and a13 are the coefficients of the first row of the matrix.
The elements a21, a22 and a23 are the coefficients of the second row of the matrix.
Note. The order of elements is crucial in a matrix in linear algebra. A different arrangement of elements generates a different matrix. For example, if I define matrix B by reversing the rows of matrix A $$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$ $$ B : = \begin{pmatrix} 0 & 4 & -1 \\ 3 & 1 & 6 \end{pmatrix} $$ the matrices A and B will have the same elements but will be different matrices. It is important to remember this.
The Sets of Matrices
The set of all mxn matrices with real elements (real matrices) is denoted by the notation Mm,n(R) or M(m,n,R).
$$ M_{m,n}(R) = M(m,n,R) $$
The set of square matrices is indicated as follows:
$$ M_{n,n}(R) = M(n,n,R) $$
Example
The matrix A is composed of 2 rows and 3 columns.
$$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$
Therefore, matrix A belongs to the set of 2x3 matrices.
$$ A \in M(2,3,R) $$
Note. The matrix A belongs to the set of 2x3 matrices with real coefficients, denoted by M(2,3,R). Therefore, its elements are not only integers but also real numbers (R). If I want to define a matrix consisting only of integers, I have to write M(2,3,Z) where Z is the set of integers. The set of matrices M(2,3,Z) is a subset of M(2,3,R) because, for matrices of the same dimensions, integers are a subset of real numbers, i.e., Z⊂R.
Types of Matrices
Based on their dimensions, number of rows and columns, I can distinguish the following types of matrices:
- Rectangular matrices. These are matrices with more than one row (m>1) and at least one column (n>0) where the number of rows is not equal to the number of columns (m≠n). The rectangular shape of these matrices is derived from this characteristic.
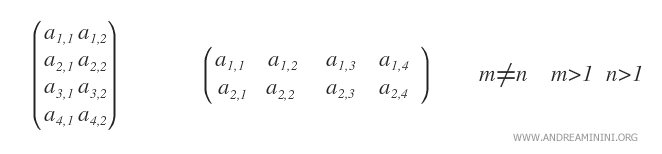
- Square matrix. A square matrix has the same number of rows and columns (m=n), giving it a square shape.
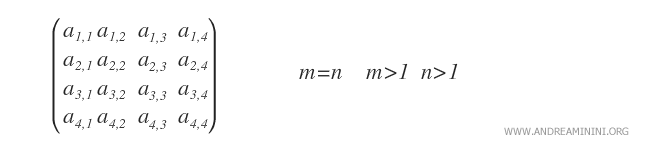
- Row matrix. A row matrix is a 1xn matrix with only one row (m=1).
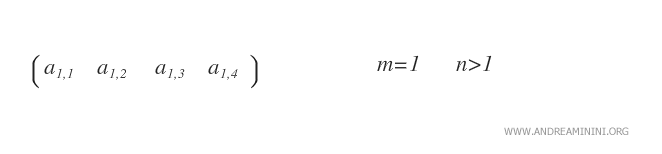
- Column matrix. A column matrix is an mx1 matrix with only one column (n=1).
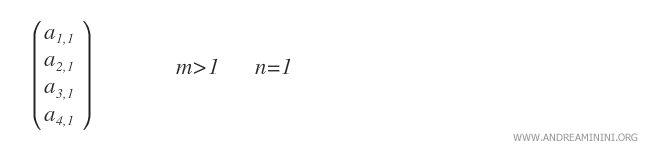
- Empty matrix. These are matrices with no elements at all - no rows (m = 0) and no columns (n = 0). They are also referred to as 0×0 zero matrices.
How to represent a linear system with a matrix
Given a linear system A composed of m equations and n variables
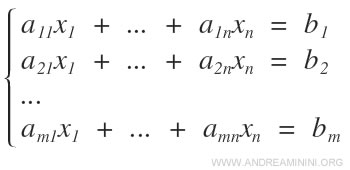
the linear system can always be associated with two matrices:
- The coefficient matrix (or incomplete matrix) is an m-by-n matrix, in which the elements are the coefficients amn of the equations in the linear system.
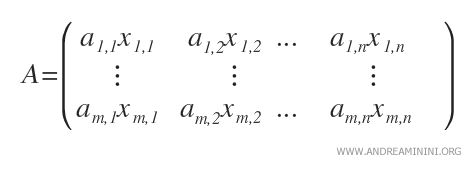
- The augmented matrix (or complete matrix) is a matrix consisting of m rows and n+1 columns, composed of both the coefficients amn and the constants bm of the linear system. This matrix combines the coefficient matrix A with the column vector of constants B. It's also known as the augmented matrix form, bordered or edged matrix of the system AX.
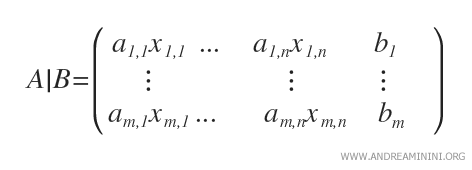
Note. Essentially, the augmented matrix is the coefficient matrix with the addition of the column of constants terms, when dealing with matrices and equations in linear algebra.
A Practical Example of Matrices and Equations in Linear Algebra
This linear system consists of two equations and three variables. The coefficient matrix A is as follows:
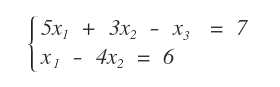
The coefficient matrix A is as follows:
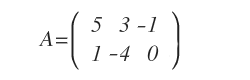
Note. In the second equation of the system (x1-4x2=6), the variable x3 is not present. In such cases, the corresponding element of the matrix is assigned a value of zero.
The complete matrix A|B of the system is as follows:
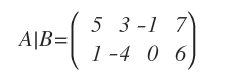
Nota. I simply added the column of constants to the coefficient matrix.
And so on
