Matrix power

The power of a matrix is calculated by multiplying the matrix by itself, combining rows and columns in succession.

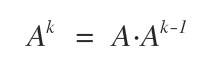
For a square matrix \( A \) of order \( n \) and a non-negative integer \( k \), the power \( A^k \) is obtained by multiplying \( A \) by itself \( k-1 \) times.

Note: Matrix exponentiation does not involve raising each element to the power individually. This only occurs in certain cases, such as with diagonal matrices.

Example of Matrix Exponentiation

Consider the square matrix \( A \) of order 2 below. Let’s calculate its cube.

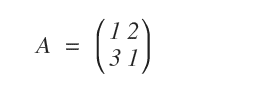
To find the cube of the matrix, we multiply it by itself three times.

The following shows how to calculate this exponentiation.

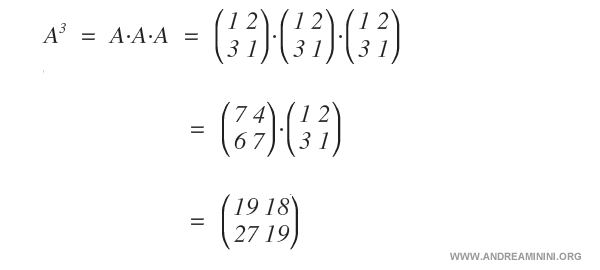
Note: As you can see, \( A^3 \) does not result in each element being raised to the third power, due to the properties of matrix multiplication (row by column), which differ from those of standard multiplication.

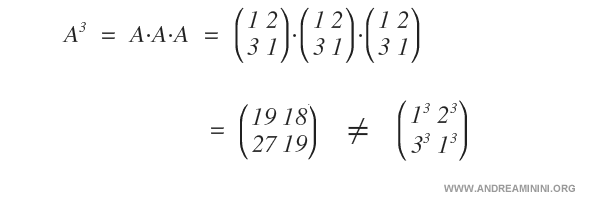
Nilpotent and Idempotent Matrices

A square matrix \( A \) of order \( n \) is called nilpotent of order \( k \) if \( A^k \) results in the zero matrix (O).

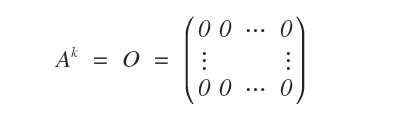
The matrix below is an example of a nilpotent matrix.

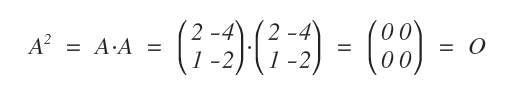
Similarly, a square matrix \( A \) of order \( n \) is termed idempotent if \( A^k = A \) for some positive integer \( k \).

Below is a practical example of an idempotent matrix.

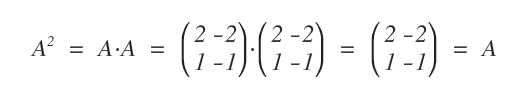
Note: Nilpotent and idempotent matrices appear only under row-column multiplication rules.

The Zero Power of a Matrix

Any square matrix of order \( n \) raised to the power of zero results in the identity matrix \( I \) of the same order.

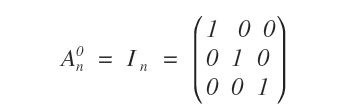
The Power of a Matrix with a Negative Exponent

When the exponent \( k \) is negative, the power of matrix \( A \) is calculated by multiplying its inverse \( A^{-1} \) \( |k| \) times.

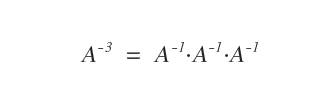
Diagonal Matrices

In the case of diagonal matrices, the matrix power equals the power of each individual element. This is a unique case.

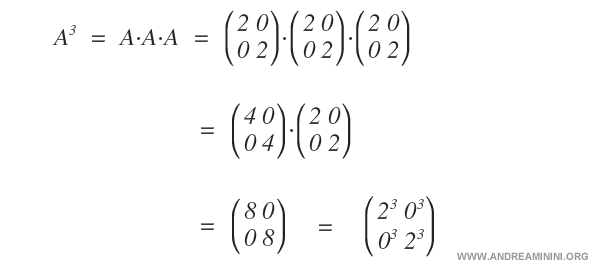
For other matrices, the power of the matrix does not correspond to the power of its elements.

Matrix Binomial Powers

The binomial power rule for real numbers does not apply to matrices. Matrix exponentiation follows different principles.

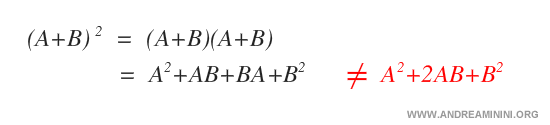
Note: This is yet another example of how matrix powers differ from the powers of real numbers, requiring a distinct calculation process.