Antisymmetric matrices

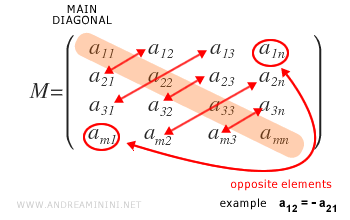
A matrix M is called antisymmetric if its elements above the main diagonal are equal in magnitude but have opposite signs to the corresponding elements below the diagonal.

We denote an antisymmetric matrix as A^SM, where AS stands for Anti Symmetric.

Example of an antisymmetric matrix: This 3x3 matrix illustrates an antisymmetric matrix, where each element a_ij matches the corresponding element a_ji but with the opposite sign.

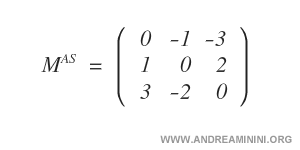
The element a_ij is simply found by swapping the row and column indices (a_ij ⇒ a_ji).

In an antisymmetric matrix, for any i and j from 1 to n, elements are related by a_ij = -a_ji.

Relationship between an antisymmetric matrix and its transpose

If a matrix is antisymmetric, its transpose M^T is equal to -M.

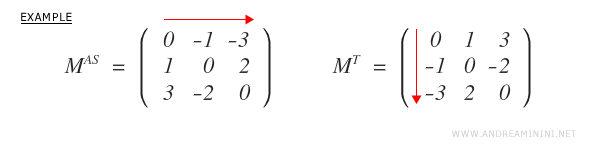
Only square matrices can be antisymmetric

Rectangular matrices cannot be antisymmetric since their transposes have different dimensions than the original matrix.

Additionally, rectangular matrices lack a main diagonal.

The zero diagonal in antisymmetric matrices

In an antisymmetric matrix, all elements on the main diagonal are zero.

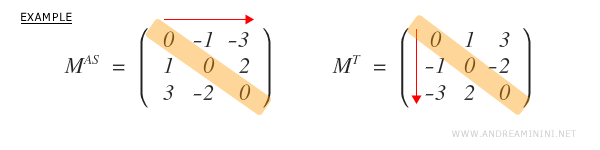
Why is the diagonal zero in antisymmetric matrices? The diagonal elements must be zero because, in the transpose of a square matrix, diagonal values (a_ij = a_ji) stay the same, and zero is the only value equal to its own opposite.

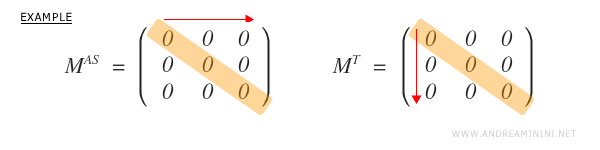
Can a matrix be both symmetric and antisymmetric?

The zero matrix is the only matrix that can be both symmetric and antisymmetric.

How to calculate an antisymmetric matrix

Any square matrix can be converted to an antisymmetric matrix.

To find the antisymmetric form of a square matrix M, we use this formula:

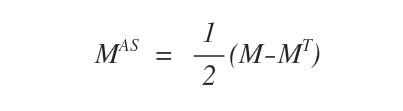
A practical example

Consider this 3x3 matrix, which is square but not antisymmetric.

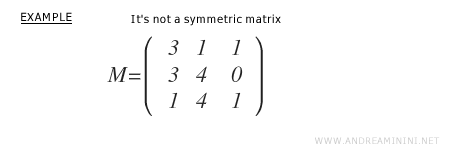
To find its antisymmetric form, we first calculate its transpose M^T.

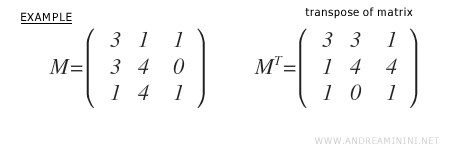
Then, we apply the formula 1/2·(M - M^T).

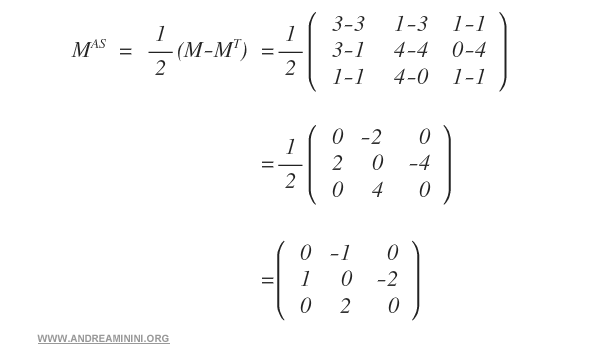
This gives the antisymmetric matrix A^AS for matrix M, where the main diagonal is zero and opposite elements are symmetrically positioned across it.

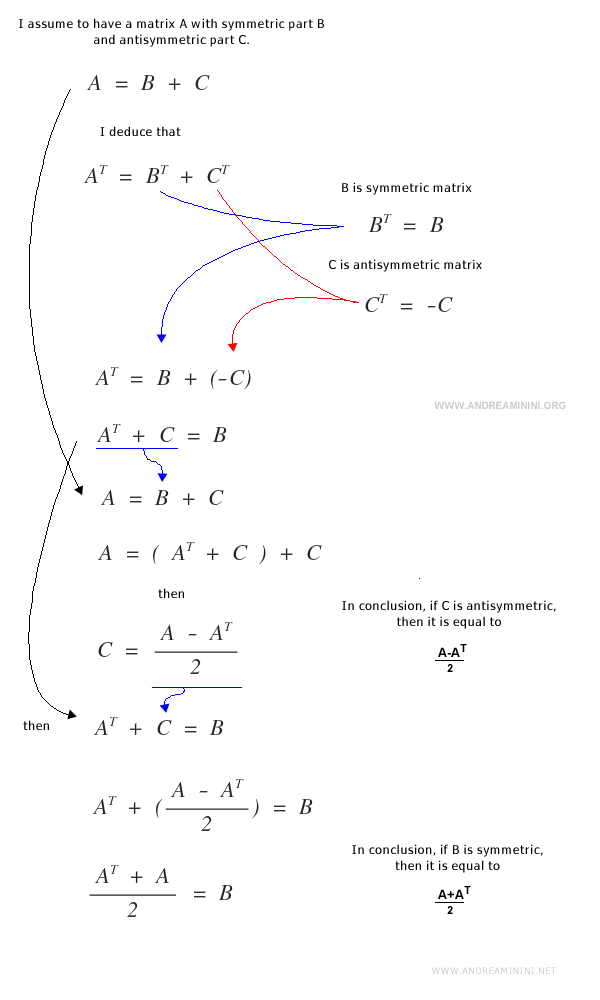
The sum of symmetric and antisymmetric matrices

The sum of the symmetric matrix M^S and the antisymmetric matrix M^AS equals the original matrix M.

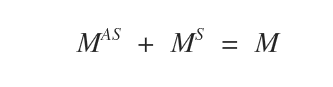
Note: M^AS is called the antisymmetric part of M, while M^S is the symmetric part. If M is symmetric, then its antisymmetric part is zero; similarly, if M is antisymmetric, its symmetric part is zero.

Let’s go through a practical example of calculating both the symmetric and antisymmetric parts for this square matrix.

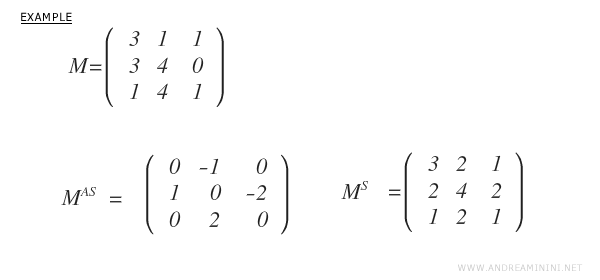
The sum of M^AS and M^S gives the original matrix M.

 

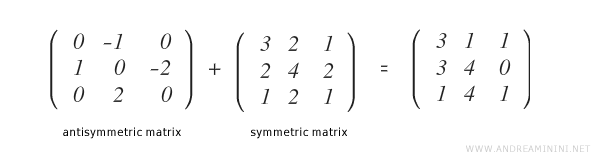
Proof:

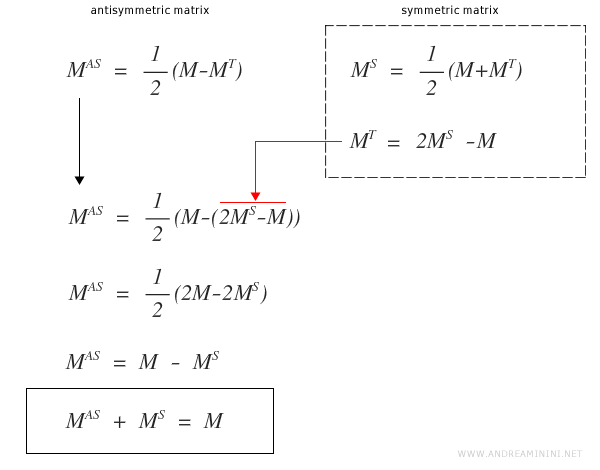
Proving the uniqueness of the symmetric and antisymmetric parts requires a bit more detail.