Diagonal Matrix

A square matrix is known as a diagonal matrix when all elements outside the main diagonal are zero.

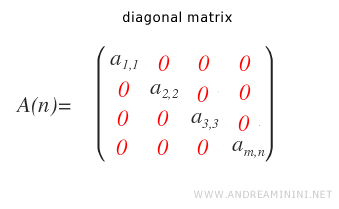
In other words, if \( i \neq j \), then \( a_{ij} = 0 \).

Example

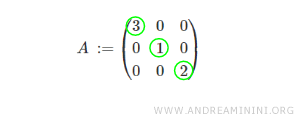
For example, consider a diagonal matrix of order 3, which has three rows and three columns.

As shown, all elements above and below the main diagonal are zero.

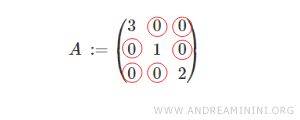
Note: Elements on the main diagonal may be either zero or non-zero.

Therefore, a diagonal matrix can also be considered both a lower and an upper triangular matrix.

In mathematics, the set of diagonal matrices of order \( n \) with real-number entries is denoted by \( D \), where \( n \) indicates the matrix order and \( R \) represents real coefficients.

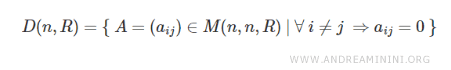
In summary, diagonal matrices are fundamental in linear algebra, with applications spanning various branches of mathematics and science.