Pivot operation in a matrix

The pivot operation is a matrix computation that transforms an m x n matrix by replacing its k-th column with the h-th column of an m x m identity matrix.

To perform a pivot operation, you first select a non-zero matrix element, known as the pivot element. If an element is zero, it cannot serve as the pivot.

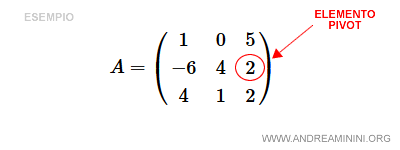
The pivot operation consists of two key steps:

1. Divide all entries in the h-th row by the pivot element (a_hk) so that the pivot element becomes 1: $$ \bar{a}_{h} = \frac{a_{hi}}{a_{hk}} $$
2. Subtract the pivot row, scaled by the element in the pivot column (a_jk), from every other row j: $$ \bar{a}_{j} = a_{j} - a_{jk} \cdot \bar{a}_{h} $$ This eliminates all entries in the pivot column except the pivot element itself.

A Practical Example

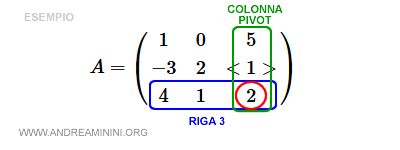
Consider the following matrix:

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & 2 \\ 4 & 1 & 2 \end{pmatrix} $$

Here, we’ll use a₂₃, the third element in the second row, as the pivot element.

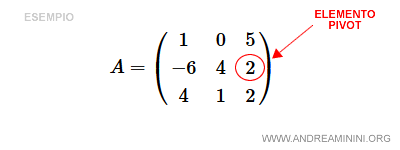
This makes the third column our pivot column and the second row our pivot row.

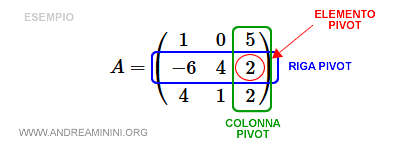
To highlight the pivot element, we’ll enclose it in <> symbols:

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & <2> \\ 4 & 1 & 2 \end{pmatrix} $$

Next, we divide each entry in the pivot row by the pivot element, a₂₃ = 2:

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ \frac{-6}{2} & \frac{4}{2} & <\frac{2}{2}> \\ 4 & 1 & 2 \end{pmatrix} $$

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -3 & 2 & <1> \\ 4 & 1 & 2 \end{pmatrix} $$

The pivot row is now updated, with the pivot element scaled to 1.

Then, for each other row, we subtract the pivot row, scaled by the corresponding entry in the pivot column (k=3).

Row 1

The first row is [1, 0, 5], with 5 as the entry in the pivot column (k=3).

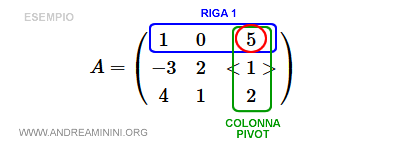
$$ a_1 = [ 1 \:\: 0 \:\: 5] - 5 \cdot [-3 \:\: 2 \:\: 1] $$

$$ a_1 = [ 1 \:\: 0 \:\: 5] - [-15 \:\: 10 \:\: 5] $$

$$ a_1 = [ 16 \:\: -10 \:\: 0] $$

Row 2

The second row is the pivot row and does not need any further modification.

Row 3

The third row is [4, 1, 2], with 2 as the entry in the pivot column (k=3).

$$ a_1 = [ 4 \:\: 1 \:\: 2] - 2 \cdot [-3 \:\: 2 \:\: 1] $$

$$ a_1 = [ 4 \:\: 1 \:\: 2] - [-6 \:\: 4 \:\: 2] $$

$$ a_1 = [ 10 \:\: -3 \:\: 0] $$

With these adjustments, we’ve updated the first and third rows accordingly.

The Final Result

After completing the pivot operation on a₂₃, our matrix is:

$$ A = \begin{pmatrix} 16 & -10 & 0 \\ -3 & 2 & <1> \\ 10 & -3 & 0 \end{pmatrix} $$

The pivot element has been scaled to 1, and all other entries in the pivot column are zero.

An Alternative Approach

Another way to perform the pivot operation involves using an m x m identity matrix.

Given a matrix M of dimensions m x n and a pivot element a_h,k, we can follow these steps:

1. Create an identity matrix Q of dimensions m x m.
2. Replace the h-th column of Q with the k-th column of M.
3. Substitute the pivot element a_h,k in Q with its reciprocal.
4. Multiply all other entries in Q’s pivot column by the negative reciprocal of the pivot element.
5. Multiply Q by M to obtain M' = Q x M.
6. The resulting matrix M' reflects the pivot operation.

Practical Example

Let’s apply this alternative method to matrix A from our previous example.

This matrix has m=3 rows and n=3 columns, with the pivot element a_2,3=2.

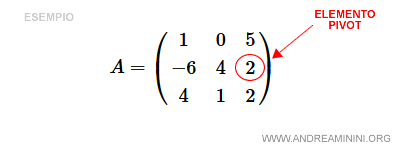
Start with the identity matrix Q (3 x 3):

$$ Q = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Replace the h=2 column in Q with the k=3 column of A, marking the pivot element with <>:

$$ Q = \begin{pmatrix} 1 & 5 & 0 \\ 0 & <2> & 0 \\ 0 & 2 & 1 \end{pmatrix} $$

Next, replace the pivot element in Q with its reciprocal:

$$ Q = \begin{pmatrix} 1 & 5 & 0 \\ 0 & \frac{1}{<2>} & 0 \\ 0 & 2 & 1 \end{pmatrix} $$

Multiply the other entries in column h=2 by the negative reciprocal of the pivot element:

$$ Q = \begin{pmatrix} 1 & -\frac{5}{2} & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & -1 & 1 \end{pmatrix} $$

Now, multiply Q by A:

$$ Q \cdot A = \begin{pmatrix} 1 & -\frac{5}{2} & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & 2 \\ 4 & 1 & 2 \end{pmatrix} $$

$$ Q \cdot A = \begin{pmatrix} 16 & -10 & 0 \\ -3 & 2 & <1> \\ 10 & -3 & 0 \end{pmatrix} $$

The outcome is the same as before, completing the pivot operation.