Equivalent Matrices
Two matrices are considered equivalent if they share the same solution set, S, for their associated linear systems.
Example

The equivalence of two matrices, M and M', is denoted by the tilde symbol (~).
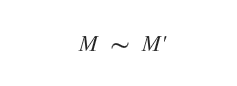
Example
Matrices are often used to represent systems of linear equations.

Reordering the equations in a linear system does not alter the solution set.
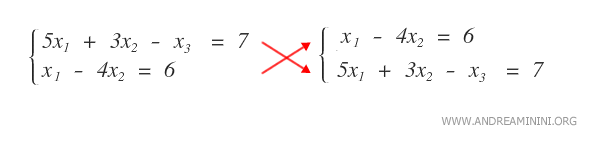
Likewise, changing the row order in a matrix produces an equivalent matrix.
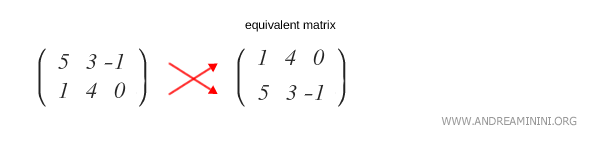
Note: This is a simplified example for clarity. In practice, equivalent matrices may have entirely different values for their elements. Several methods exist for matrix transformations, with Gaussian elimination and Gauss-Jordan elimination being the most widely used.
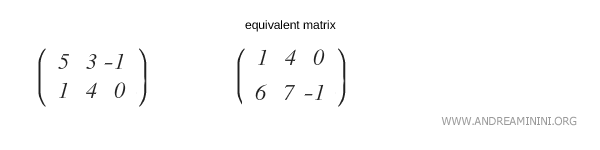
Constructing an Equivalent Matrix
Using Gaussian elimination, any matrix M can be transformed into an equivalent matrix M' through a sequence of permitted operations, known as Gaussian moves.
- Interchanging rows in the matrix
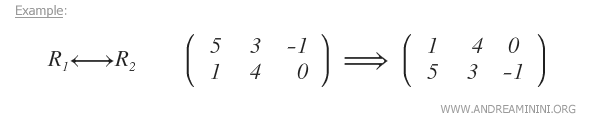
- Multiplying a row by a nonzero real number α
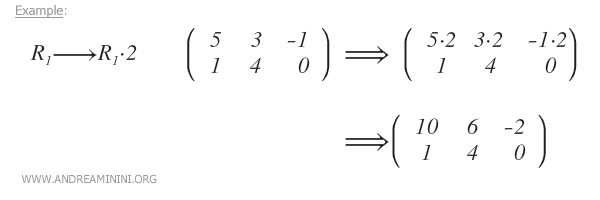
- Adding corresponding elements from two rows
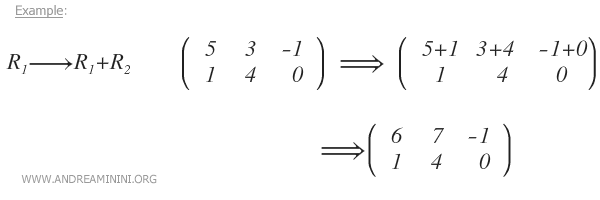
If two polynomials have a shared root, that root will remain in the sum. Therefore, the solutions of the original polynomials are also solutions in their sum.
Note: These operations can also be applied in combination. For example, a row may be added to another row multiplied by a real number.
