Triangular Matrix

A square matrix is called a triangular matrix if all its nonzero elements are either above or below the main diagonal.

Types of Triangular Matrices

Triangular matrices are classified as either upper or lower:

• Upper Triangular. All nonzero elements appear above the main diagonal, with the diagonal itself possibly containing nonzero entries.
  
  

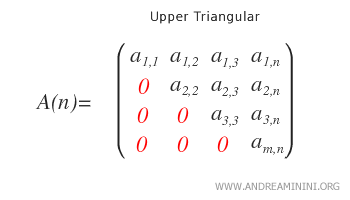
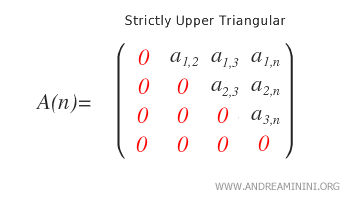
  Strictly Upper Triangular. A matrix is strictly upper triangular if all nonzero elements lie strictly above the main diagonal, while every element on the diagonal is zero. In other words, for all entries \( a_{ij} \), we have \( i < j \), meaning the main diagonal and everything below it consists of zeros.
  

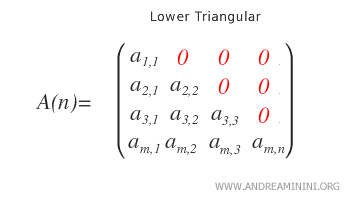
• Lower Triangular. A matrix is lower triangular if all nonzero elements appear below the main diagonal, with the diagonal itself possibly containing nonzero entries.
  
  

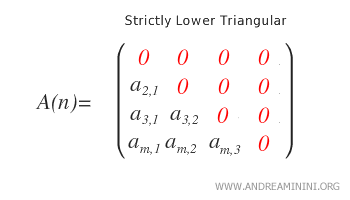
  Strictly Lower Triangular. A matrix is strictly lower triangular if all nonzero elements are located strictly below the main diagonal, while the diagonal itself consists entirely of zeros.
  

Properties of Triangular Matrices

Some key properties of triangular matrices:

• Determinant
  The determinant of a triangular matrix is simply the product of its diagonal elements.

  Example. The following square matrix is triangular: $$ A = \begin{pmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{pmatrix} $$ Its determinant is given by the product of its diagonal elements, as all other terms contribute zero: $$ \det(A) = 2 \cdot 1 \cdot 5 \cdot 2 = 20 $$

And so on...