Lower Triangular Matrix

A square matrix is called a lower triangular matrix if all the elements above the main diagonal are zero: $$ \forall \ i < j \ \ \ \ a_{ij } = 0 $$

A Practical Example

Here’s an example of a 3×3 lower triangular matrix, with three rows and three columns.

All the elements above the main diagonal are zero.

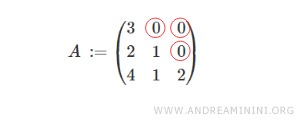
Note: The other elements of the matrix don’t necessarily have to be nonzero - they can be zero as well.

If the main diagonal consists entirely of zeros, the lower triangular matrix is called a strictly lower triangular matrix.

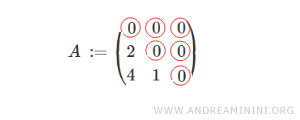
The set of lower triangular matrices with real coefficients of order \( n \) is denoted as \( T_{R} \).

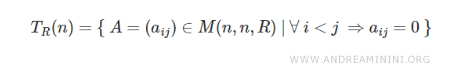
Note: Triangular matrices reduce computational complexity because data is confined to just one part of the matrix. This means fewer calculations and less memory usage.

Why Use a Lower Triangular Matrix?

The elements of a lower triangular matrix occupy only half the space of a full square matrix. This makes computations more efficient.

Additionally, the determinant of a triangular matrix is simply the product of the elements on the main diagonal, as all other terms contribute zero.

And so on.