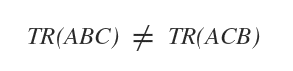Trace of a Matrix

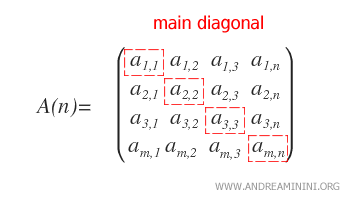
The trace of a square matrix A of size n is the sum of its elements on the main diagonal.

The formula to calculate the trace is as follows:

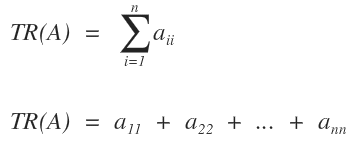
A Practical Example

The following square matrix is of order three.

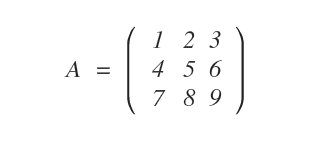
The elements on the main diagonal are 1, 5, and 9.

To calculate the trace, TR(A), I add these elements together.

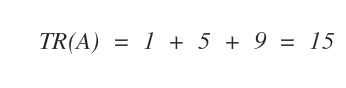
Therefore, the trace of matrix A is 15.

Properties of Matrix Trace

The trace of a matrix adheres to the following properties:

1. The trace of a scalar alpha times a matrix, TR(α·A), equals the scalar alpha times the trace of the matrix, α·TR(A).
   
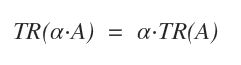
2. The sum of the traces of two matrices, TR(A)+TR(B), equals the trace of the sum of the matrices, TR(A+B).
   

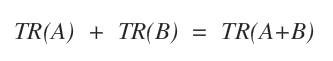
   Note. These first two properties prove that the trace is a linear function.

3. Matrix A and its transpose A^T have the same trace.
   
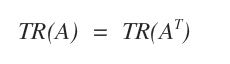
4. The trace of the product of matrices, TR(ABC), remains invariant under a cyclic permutation, TR(BCA) and TR(CAB).
   

   An example of non-cyclic permutation. The trace is not equal in TR(ACB) or TR(CBA) because these are not cyclic permutations. In these cases, the order of the factors in the product of matrices ABC is not obtained by moving the factors to the right or left.