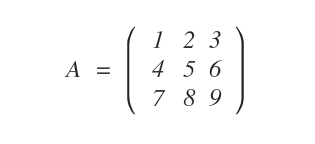Minor of a Matrix

A minor of an \( n \)-order matrix \( A \) is the determinant of a square submatrix of order \( p \) (where \( p \le n \)), formed by omitting \( m-p \) rows and \( n-p \) columns.

It’s essential to recognize that a minor represents the determinant of a specific submatrix (commonly called a cofactor matrix) and, as such, is a scalar value, not a matrix itself.

In some contexts, however, the term “minor” may also refer to the submatrix itself.

What is the order of a minor? The order of a minor corresponds to the number of rows (or columns) in the submatrix. For example, a submatrix with three rows and three columns is a third-order minor.

Calculating a Matrix Minor

To determine a minor, select \( p \) rows and \( p \) columns from matrix \( A \) to form a square submatrix.

1. Select rows \( i, j \) for removal from the matrix.
2. The resulting square submatrix is known as the cofactor matrix \( A_{ik} \).
3. The determinant of this cofactor matrix \( A_{ik} \) is the minor.

Note: The indices \( i \) and \( j \) specify which rows and columns are removed from \( A \) to create the smaller square submatrix.

For first-order minors, the minor consists of a single element.

A Practical Example

Consider the following 3x3 matrix; let’s calculate its minors.

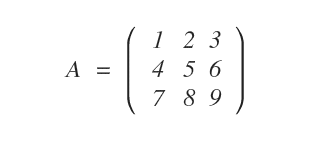
Note: While the original matrix might not always be square, each of its minors is a square matrix or a single element (order 1).

This is a third-order matrix with three rows (\( m = 3 \)) and three columns (\( n = 3 \)).

It, therefore, has minors up to order 3.

Second-Order Minors

To calculate a second-order minor (\( p = 2 \)), remove one row (\( m-p = 1 \)) and one column (\( n-p = 1 \)) from the matrix for each computation.

Then, calculate the determinant of the resulting submatrix.

Explanation: When calculating the minor \( A_{31} \), we remove the third row (7, 8, 9) and the first column (1, 4, 7) from the matrix. The remaining elements are located in rows 2 and 3 and columns 2 and 3, forming the minor \( A_{31} \). Using this same approach, other second-order minors can be calculated as well.

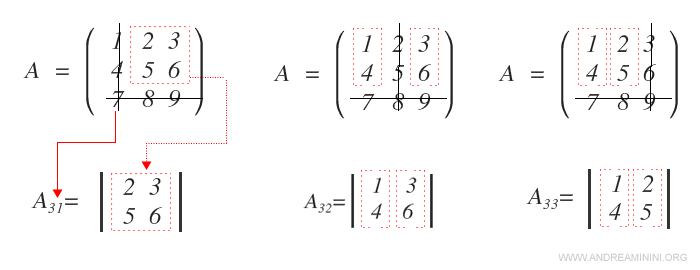
First-Order Minors

The matrix also contains nine first-order minors.

To find a first-order minor (\( p = 1 \)), remove two rows (\( m-p = 2 \)) and two columns (\( n-p = 2 \)) each time.

In this case, the minor (determinant) is simply the value of the single element in the submatrix.

Note: The third-order minor is the determinant of the full matrix. To calculate a third-order minor (\( p = 3 \)), no rows (\( m-p = 0 \)) and no columns (\( n-p = 0 \)) are removed.