Submatrices

A submatrix is created by selecting certain rows and columns from a reference matrix while keeping their original order intact.

Definition of a Submatrix: Let \( I = \{1, \dots, m\} \) and \( J = \{1, \dots, n\} \) be subsets of \( Z \), and let \( A = (a_{ij}) \) represent an \( m \times n \) matrix where \( i \in I \) and \( j \in J \). For any subsets \( H \subset I \) and \( K \subset J \), the submatrix of \( A \) is denoted as \( A_{HK} = (a_{ij}) \) where \( i \in H \) and \( j \in K \).

Practical Example of a Submatrix

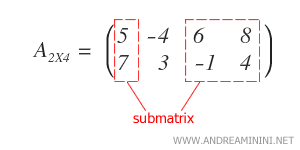
The matrix \( A_{2 \times 4} \) shown below has two rows ( \( m = 2 \) ) and four columns ( \( n = 4 \) ).

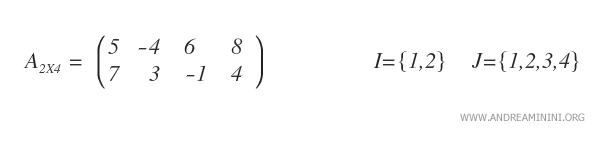
By selecting specific subsets \( H \) and \( K \) of \( I \) and \( J \), we obtain a submatrix \( A_{HK} \).

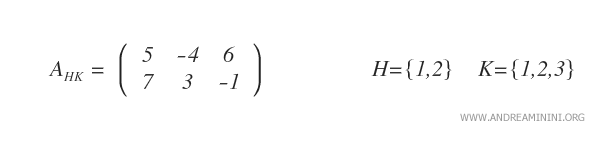
Note: Here, I chose the first three columns, leaving out the last one.

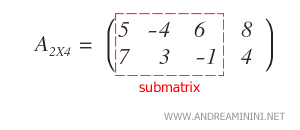
It’s important to note that the rows and columns selected don’t have to be contiguous.

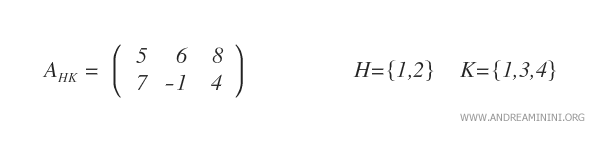
Note: In this example, I formed the submatrix by choosing the first, third, and fourth columns.

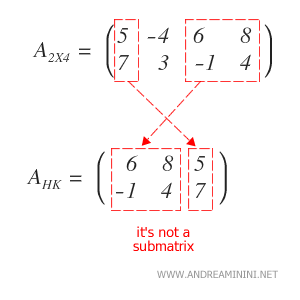
The essential point is that the submatrix preserves the row and column order from the original matrix.

Example: If the column order is altered, the resulting matrix is no longer a true submatrix, even if it contains the same elements. This is not a submatrix because the column order differs.