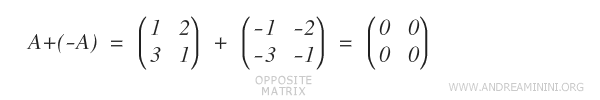Matrix addition

How to Add Two Matrices

To add two matrices, A and B, with the same dimensions (m rows by n columns), simply add each pair of corresponding elements (a_ij + b_ij) to form a new matrix.

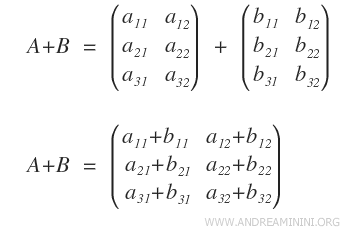
Can you add matrices with different dimensions? No, you cannot add matrices that have a different number of rows (m) or columns (n).

Example of Matrix Addition

In this example, we have two matrices, A and B.

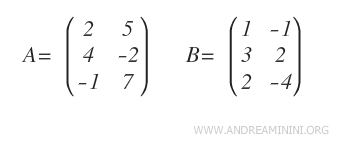
Since both matrices have the same dimensions (3x2), we can add them to get matrix A + B.

The resulting matrix, A + B, is created by adding each corresponding element from matrices A and B.

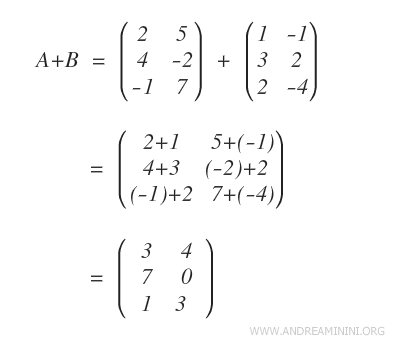
This gives us the final sum matrix.

Properties of Matrix Addition

Matrix addition follows these key properties:

1. Associativity
   For any three matrices, the sum A + (B + C) is the same as (A + B) + C.
2. Commutativity
   For any two matrices, A + B equals B + A.
   
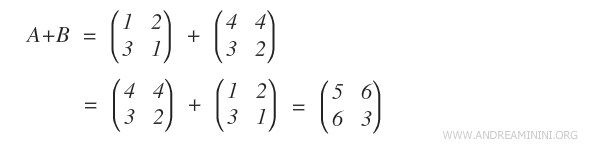
3. Existence of a Neutral Element
   In matrix addition, there is a neutral element represented by matrix O. Adding O to any matrix A leaves A unchanged.
   

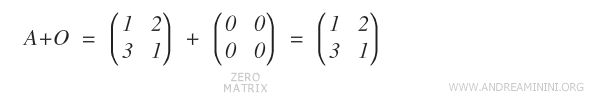
   Note: The neutral matrix is an m x n matrix where every element is zero.

4. Existence of an Opposite Element
   For every matrix A, there exists an opposite matrix, -A, such that A + (-A) results in the zero matrix (O).