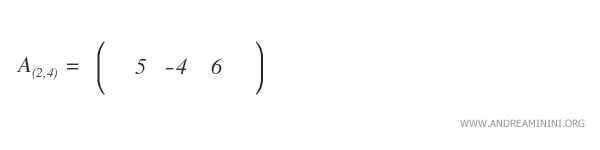Complementary Submatrix

The complementary submatrix of an element \( a_{ij} \) is the smaller matrix created by removing the i-th row and j-th column from the original matrix.

This complementary submatrix is denoted by \( A_{(ij)} \).

Note: The complementary submatrix is a specific type of submatrix in which only one row and one column are omitted.

A Practical Example

Let’s consider a matrix \( A_{2x4} \) with two rows (m=2) and four columns (n=4).

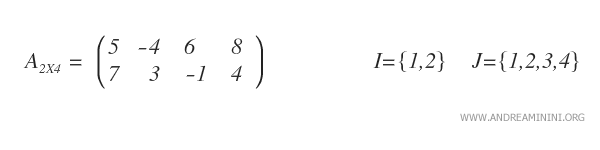
We’ll determine the complementary submatrix for the element \( a_{2,4} \), which is the bottom-right entry (value 4).

To obtain this, we remove the second row and the fourth column.

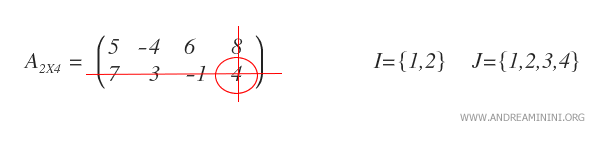
This gives us the complementary submatrix, represented as \( A_{(2,4)} \).