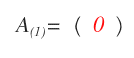Square matrix

A Square Matrix is one with an equal number of rows and columns (m = n). This type of matrix is known as a matrix of order n and is commonly represented by the symbol A(n).

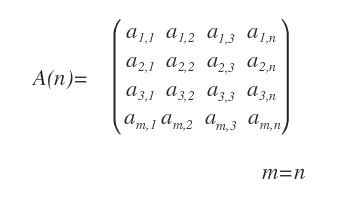
Applications of Square Matrices Square matrices have specific properties that make them particularly valuable in Linear Algebra.

Diagonals of a Square Matrix

Square matrices feature two distinct diagonals:

1. Main Diagonal: For a square matrix of order n, the main diagonal consists of elements a_i,i where i = 1, ..., n. It runs from the top-left to the bottom-right.
   
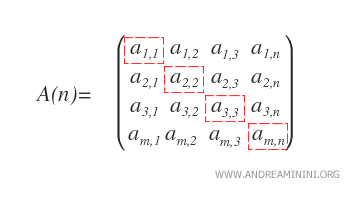
2. Secondary Diagonal: This diagonal consists of elements a_i,i for i = n, ..., 1 and extends from the top-right to the bottom-left.
   

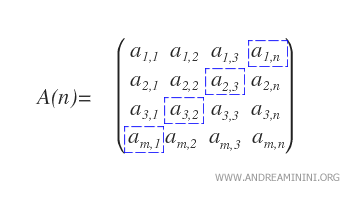
Note: Only square matrices have diagonals; rectangular, row, column, and null matrices lack diagonals.

Diagonal, Upper Triangular, and Lower Triangular Matrices

Square matrices can also be categorized as diagonal, upper triangular, or lower triangular:

• Upper Triangular Matrices: A matrix is upper triangular if a_ij = 0 for every i > j, meaning all elements below the main diagonal are zero.
  
  

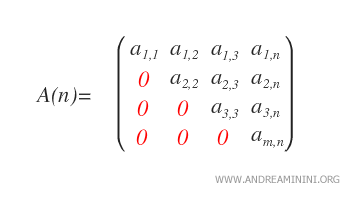
  The set of real upper triangular matrices of order n is denoted by U_n(R).

  Strictly Upper Triangular Matrices: A matrix is strictly upper triangular if a_ij = 0 for every i ≥ j, including all elements on and below the main diagonal.
  
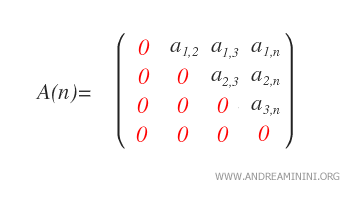
  The set of strictly upper triangular matrices of order n is represented as U*_n(R).

• Lower Triangular Matrices: A matrix is lower triangular if a_ij = 0 for every i < j, indicating that all elements above the main diagonal are zero.
  
  

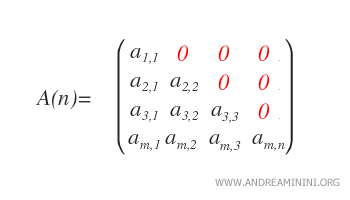
  The set of real lower triangular matrices of order n is designated as L_n(R).

  Strictly Lower Triangular Matrices: A matrix is strictly lower triangular if a_ij = 0 for every i ≤ j, including elements on and above the main diagonal.
  
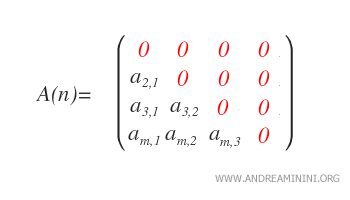
  This set is represented by L*_n(R).

• Diagonal: A square matrix is diagonal if a_ij = 0 for every i ≠ j, meaning all elements outside the main diagonal are zero. Thus, a diagonal matrix is both upper and lower triangular.
  
  

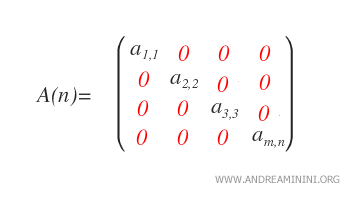
  The set of n x n real diagonal matrices is denoted by D_n(R).

Note: An upper or lower triangular classification does not require other elements to be nonzero.

Special Types of Square Matrices in Linear Algebra

The zero matrix is a notable case, as it is simultaneously lower triangular, upper triangular, strictly lower and upper triangular, and diagonal.

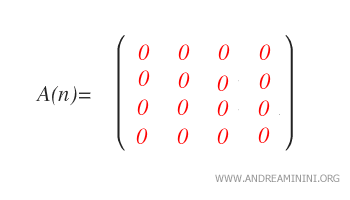
Another unique case is the square matrix of order 1, which consists of just one element, a_1,1.

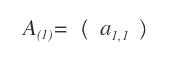
By definition, a square matrix of order 1 is always lower triangular, upper triangular, and diagonal.

Note: If a_1,1 = 0, the square matrix of order 1 is also strictly lower and upper triangular.