Identity matrix

An identity matrix of order \( n \) is a square diagonal matrix where each entry along the main diagonal is one, and all other entries are zero. Because of this, it’s also known as a unit matrix or simply an identity matrix.

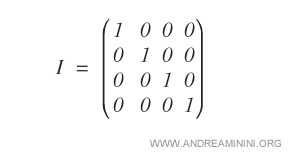
This matrix is a specific case of diagonal matrices, with unique properties.

The identity matrix is represented by \( I_{(n)} = (\delta_{ij}) \), where \( n \) denotes its order, and the elements \( \delta_{ij} \) are called the Kronecker delta.

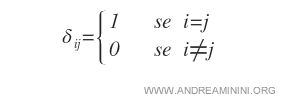
Note: The identity matrix is also a particular instance of a scalar matrix, where all diagonal elements equal one.

Properties of Identity Matrices

Here are some key properties of identity matrices:

• The identity matrix acts as the neutral element in matrix multiplication. When multiplying a matrix \( M \) with \( n \) columns by an identity matrix \( I \) of the same order, the result is \( M \) itself: $$ M \cdot I = M $$

  Example: $$ M \cdot I_2 = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$

  For rectangular matrices, it’s essential to ensure the number of columns in the first matrix matches the number of rows in the second for compatibility.
  • For any matrix \( A \) with \( n \) columns: $$ A \cdot I_n = A $$

    Example: $$ A \cdot I_2 = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} $$

  • For any matrix \( B \) with \( n \) rows: $$ I_n \cdot B = B $$

    Example: $$ I_3 \cdot A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} $$

• Identity matrices are commutative in multiplication when paired with any square matrix. If one of the matrices, \( A \) or \( B \), is an identity matrix, the product \( AB = BA \) holds, making the order of multiplication irrelevant to the outcome.

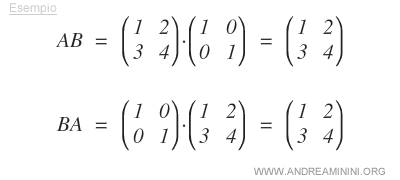
  Note: This commutative property is specific to identity matrices, as general matrices do not follow the commutative rule in matrix multiplication.

• The determinant of an identity matrix is always 1: $$ \text{det} (I) = 1 $$