Singularity of a Matrix

The singularity of a matrix is a feature that relates to the determinant of a square matrix.

What Defines a Singular Matrix?

A square matrix A is deemed singular if its determinant, det(A), equals zero. In other words, the determinant of a singular square matrix is zero.

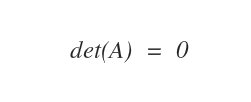
The Non-Singular Matrix

Conversely, a square matrix A is non-singular if its determinant, det(A), is not zero.

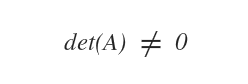
What's the Point of Matrix Singularity?

Whether a square matrix is singular or not serves as a clue to discern if the matrix is invertible.

A square matrix is invertible if and only if the matrix is non-singular.