Adjugate Matrix

The adjugate matrix plays a key role in linear algebra and is used in a wide range of mathematical applications. In simple terms, the adjugate, or adjoint (sometimes called the classical adjoint), of a matrix is obtained by transposing its cofactor matrix. Mathematically, it’s commonly represented as "adj."

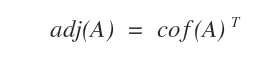
the adjugate matrix cof(A)^T

Let's walk through the process of calculating the adjugate matrix.

We’ll start with a given matrix, A:

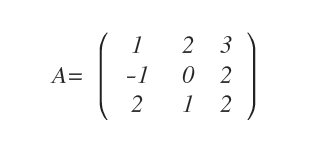
Consider the following matrix A:

To find the adjugate matrix, we first compute the matrix of cofactors of A.

Let’s take a closer look at what cofactors are. Cofactors, also known as algebraic complements, are derived from the minors of elements $ a_{ij} $ in matrix A, with each cofactor adjusted by (-1) raised to the power of $ i+j $.
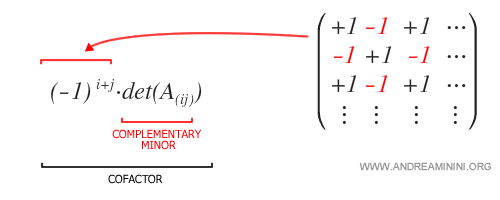
the cofactor method

To calculate the cofactor matrix, denoted $ \text{cof}(A) $, we use the following formula:

$$ \text{cof}(A) = \begin{pmatrix} (-1)^{1+1} \, \text{det}(A_{1,1}) & (-1)^{1+2} \, \text{det}(A_{1,2}) & (-1)^{1+3} \, \text{det}(A_{1,3}) \\ (-1)^{2+1} \, \text{det}(A_{2,1}) & (-1)^{2+2} \, \text{det}(A_{2,2}) & (-1)^{2+3} \, \text{det}(A_{2,3}) \\ (-1)^{3+1} \, \text{det}(A_{3,1}) & (-1)^{3+2} \, \text{det}(A_{3,2}) & (-1)^{3+3} \, \text{det}(A_{3,3}) \end{pmatrix} $$

$$ \text{cof}(A) = \begin{pmatrix} (-1)^{2} \cdot \text{det} \begin{pmatrix} 0 & 2 \\ 1 & 2 \end{pmatrix} & (-1)^{3} \cdot \text{det} \begin{pmatrix} -1 & 2 \\ 2 & 2 \end{pmatrix} & (-1)^{4} \cdot \text{det} \begin{pmatrix} -1 & 0 \\ 2 & 1 \end{pmatrix} \\ (-1)^{3} \cdot \text{det} \begin{pmatrix} 2 & 3 \\ 1 & 2 \end{pmatrix} & (-1)^{4} \cdot \text{det} \begin{pmatrix} 1 & 3 \\ 2 & 2 \end{pmatrix} & (-1)^{5} \cdot \text{det} \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} \\ (-1)^{4} \cdot \text{det} \begin{pmatrix} 2 & 3 \\ 0 & 2 \end{pmatrix} & (-1)^{5} \cdot \text{det} \begin{pmatrix} 1 & 3 \\ -1 & 2 \end{pmatrix} & (-1)^{6} \cdot \text{det} \begin{pmatrix} 1 & 2 \\ -1 & 0 \end{pmatrix} \end{pmatrix} $$

We can now evaluate these determinants and simplify the expressions.

$$ \text{cof}(A) = \begin{pmatrix} (1) \cdot (-2) & (-1) \cdot (-6) & (1) \cdot (-1) \\ (-1) \cdot 1 & (1) \cdot (-4) & (-1) \cdot (-3) \\ (1) \cdot 4 & (-1) \cdot 5 & (1) \cdot 2 \end{pmatrix} $$

After evaluating the determinants and applying the appropriate signs, we find the cofactor matrix:

$$ \text{cof}(A) = \begin{pmatrix} -2 & 6 & -1 \\ -1 & -4 & 3 \\ 4 & -5 & 2 \end{pmatrix} $$

Finally, we obtain the adjugate matrix by taking the transpose of the cofactor matrix:

$$ \text{cof}(A)^T = \begin{pmatrix} -2 & -1 & 4 \\ 6 & -4 & -5 \\ -1 & 3 & 2 \end{pmatrix} = \text{adj}(A) $$

The resulting matrix is called the adjugate (or classical adjoint) of matrix A.

Understanding how to compute the adjugate matrix is essential for solving linear systems, computing matrix inverses, and applying linear transformations.