Cofactor

The cofactor (also known as the algebraic complement) of an element \(a_{ij}\) is the minor of the submatrix \(A_{(ij)}\), multiplied by the scalar factor \((-1)^{i+j}\).

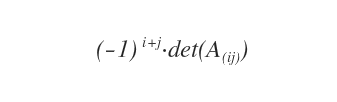
How to Calculate the Cofactor

To find the cofactor of an element in a matrix \(A\), start by calculating the minor of that element \(a_{ij}\).

What is the minor of an element? The minor of an element \(a_{ij}\) is simply the determinant of the complementary submatrix created by removing the \(i\)-th row and \(j\)-th column from the matrix.

Then, multiply this minor by \((-1)^{i+j}\).

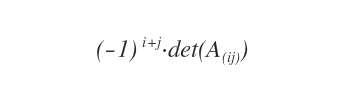
And that’s how you calculate the cofactor of \(a_{ij}\).

The sign of the cofactor depends on the position of \(a_{ij}\) within the matrix.

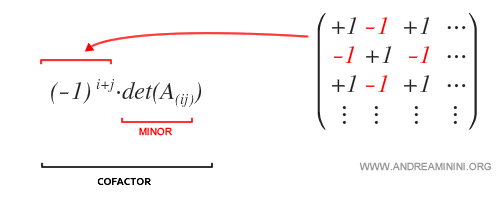
So, in some cases, the cofactor has the same sign as the minor, while in others, it has the opposite sign.

A Practical Example

Let’s consider a square matrix \(A\) of order 3.

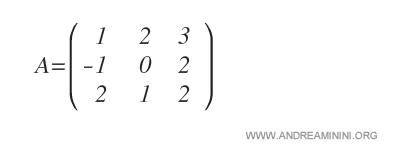
To calculate the cofactor of \(a_{11}\):

First, we extract the complementary submatrix of \(a_{11}\).

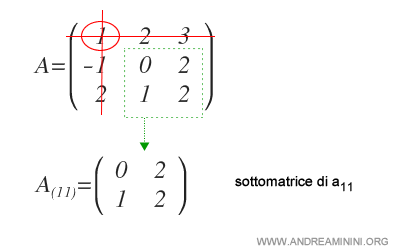
Next, we find the determinant of the submatrix \(A_{(11)}\), which gives us the minor of \(a_{11}\).

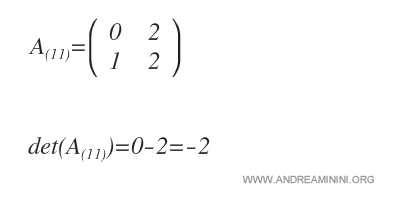
Finally, we multiply this minor by \((-1)^{i+j}\). In this case, that’s \((-1)^2\), since \(i=1\) and \(j=1\).

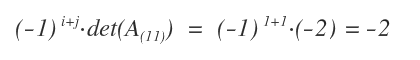
Thus, the cofactor of \(a_{11}\) is -2.

In this case, the cofactor and the minor of \(a_{11}\) are identical. However, this isn’t always true, as it depends on the position of the element.

Note: If we calculated the cofactor of \(a_{12}\), the sign would differ because \((-1)^{1+2}=-1\). The minor of \(a_{12}\) is -6, while its cofactor is 6.

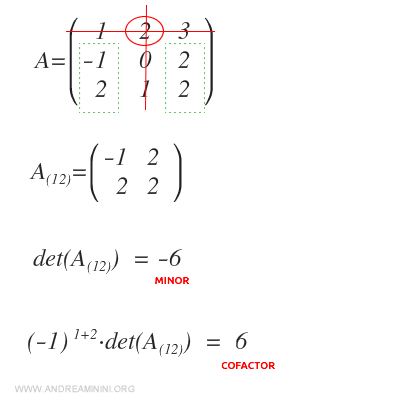
Following this method, we can find the cofactors for all other elements in the matrix.