Invertible and Inverse Matrices

In linear algebra, a square matrix $ A $ of size $ n $ is called invertible if there exists another square matrix of the same size, known as the inverse matrix and denoted $ A^{-1} $, such that $ A \cdot A^{-1} = I $ and $ A^{-1} \cdot A = I $, where $ I $ is the identity matrix (Identity Matrix).

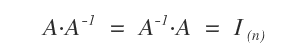
invertible matrix

In linear algebra notation, matrix inverses are represented by the superscript -1, much like the notation for reciprocals in arithmetic.

Note. The concept of a matrix inverse parallels that of a reciprocal for real numbers: every non-zero real number has a reciprocal, $ \frac{1}{a} $, such that $ a \cdot \frac{1}{a} = 1 $. Similarly, an invertible matrix $ M $ has an inverse $ M^{-1} $ satisfying $ M \cdot M^{-1} = I $, where $ I $ functions like the number 1 in real numbers, because multiplying any matrix $ M $ by $ I $ yields $ M $ itself: $ M \cdot I = M $.

Not all matrices are invertible. In fact, many matrices do not have inverses.

The collection of all invertible $ n \times n $ matrices with real entries is denoted $ \text{GL}_n(\mathbb{R}) $ or $ \text{GL}(n, \mathbb{R}) $.

$$ \text{GL}(n, \mathbb{R}) $$

This collection is also known as the general linear group of order $ n $ over the real numbers.

Note. The set $ \text{GL}_n(\mathbb{R}) $ is closed under matrix multiplication, meaning that multiplying any two invertible matrices of the same order results in another invertible matrix. Additionally, the identity matrix $ I $ is part of $ \text{GL}_n(\mathbb{R}) $.

Practical Example of Inverse Matrices
Calculating the Inverse Matrix: Two Approaches
Properties of Inverse Matrices

Practical Example of Inverse Matrices

Consider the following matrix:

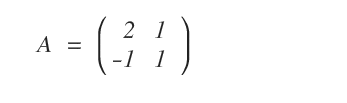
a matrix

This matrix is invertible, meaning it has an inverse $ A^{-1} $, so that multiplying $ A $ by $ A^{-1} $ yields the identity matrix $ I_{(2)} $ of the same size.

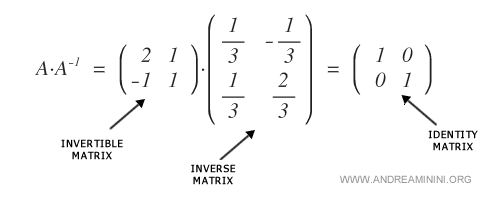
example

Calculating the Inverse Matrix: Two Approaches

There are two primary methods to find the inverse of an invertible matrix:

Note. The second method generally requires fewer calculations, making it more efficient, but the first method provides useful insights into the relationship between matrices and linear systems.

Method 1

Given a matrix $ A $, we aim to determine if it’s invertible, and if so, to calculate its inverse $ A^{-1} $.

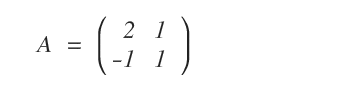
Example of a matrix:

If $ A $ is invertible, the equation $ A \cdot A^{-1} = I $ holds.

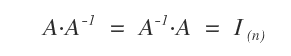
Invertible matrix:

To check if $ A $ is invertible, we multiply it by a matrix $ B $ with unknowns and set this product equal to the identity matrix $ I $.

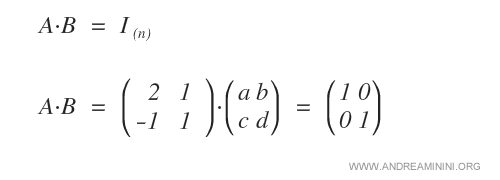
Product of matrix A by a matrix of unknowns equals the identity matrix.

Next, we carry out the row-by-column multiplication to produce a system of linear equations.

The system of linear equations equivalent to the matrix.

By solving this system, we can determine the elements of the inverse matrix, confirming $ A $ as invertible if a solution exists.

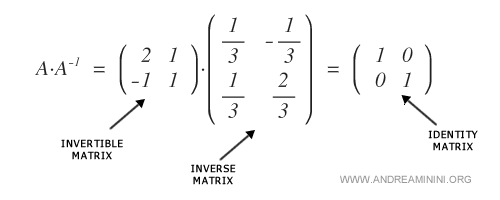
Calculation of the inverse matrix:

Note. While insightful, this method can become cumbersome for matrices larger than 2x2. The second method is preferred for higher-order matrices.

Method 2

For a 1x1 matrix, the inverse is $ A^{-1} = a_{11}^{-1} $. For larger matrices, the inverse is computed as $ A^{-1} = \frac{1}{\det(A)} \cdot \text{adj}(A) $, where $ \text{adj}(A) $ is the adjugate matrix.

The Existence Theorem states that a matrix is invertible if and only if its determinant is non-zero.

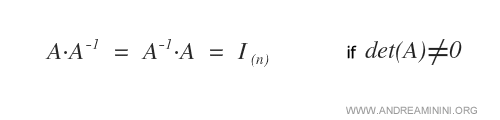
Theorem of existence of inverse matrix:

With a non-zero determinant, $ A $ is confirmed invertible. Then, we calculate the cofactor matrix, transpose it to obtain the adjugate, and multiply by $ \frac{1}{\det(A)} $ to find $ A^{-1} $.

Note. If $ \det(A) = 0 $, the matrix is non-invertible, and the calculations end here.

Properties of Inverse Matrices

Only square matrices can be invertible. If a matrix has an inverse, that inverse is unique.
The inverse matrix is not simply the reciprocal of individual elements; rather, its elements may vary widely from those of $ A $ and may even be identical to $ A $ in certain cases. Notably, the inverse of the identity matrix is the identity matrix itself.
If $ A $ is invertible, then $ A^{-1} $ is also invertible, and $ (A^{-1})^{-1} = A $.
The determinant of $ A^{-1} $ is the reciprocal of $ A $’s determinant: $ \det(A^{-1}) = \frac{1}{\det(A)} $.
If $ A $ is invertible, its transpose $ A^{T} $ is also invertible, with $ (A^{T})^{-1} = (A^{-1})^{T} $.
If matrices $ A $ and $ B $ are both invertible, then their product $ AB $ is also invertible, with $ (AB)^{-1} = B^{-1}A^{-1} $.
A matrix with a zero determinant is not invertible; only nonsingular matrices (those with a non-zero determinant) have inverses.
If a matrix has an inverse, it is guaranteed to be unique.