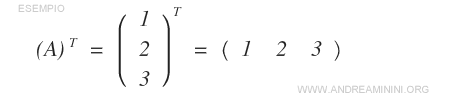Transpose of Matrices
What is the transpose of a matrix?
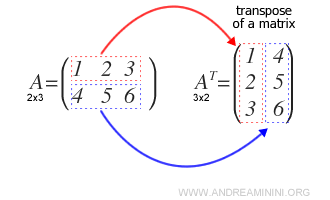
The transpose of a matrix is created by converting each row into a column. For a real matrix \( A = (a_{ij}) \) with \( m \) rows and \( n \) columns (m x n), the transpose of \( A \), denoted as \( A^T \), has \( n \) rows and \( m \) columns (n x m).
![]()
Example: To find the transpose \( A^T \) of a matrix \( A \), write each row as a column, resulting in the transpose of \( A \).
The transpose of a matrix is represented by \( A^T \). This notation is specific to the operation and should not be confused with exponentiation.
In some contexts, alternative notations for the transpose may appear, such as \( t(A) \), \( A^t \), or \( ^tA \).
Properties of the Transpose of a Matrix
The transpose operation has several important properties:
- The transpose of the sum of two matrices, \( (A + B)^T \), is equal to the sum of their transposes: \( A^T + B^T \).
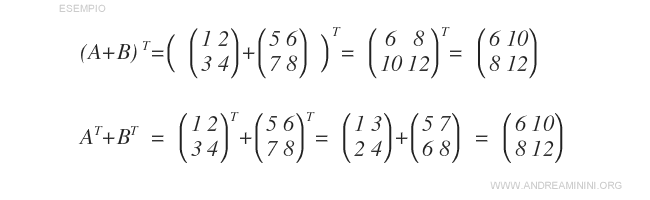
- The transpose of a scalar multiple of a matrix, \( (\alpha A)^T \), equals the scalar multiplied by the transpose of \( A \): \( \alpha A^T \).
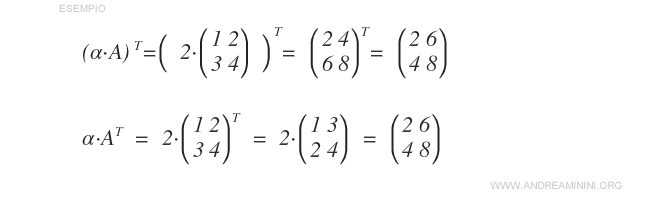
- The transpose of the transpose of a matrix returns the original matrix, i.e., \( (A^T)^T = A \).
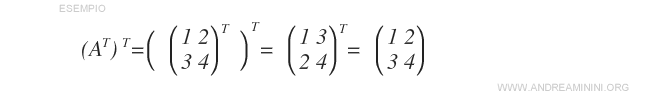
Note: This property describes an “involutive” function.
Special Cases
- A \( 1 \times 1 \) matrix is always equal to its transpose.
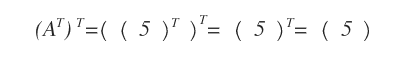
- The transpose of a row matrix \( A \) of size \( 1 \times n \) becomes a column matrix of size \( n \times 1 \).
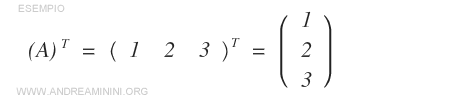
- The transpose of a column matrix \( A \) of size \( m \times 1 \) becomes a row matrix of size \( 1 \times m \).