Symmetric matrix

What is a symmetric matrix?

A symmetric matrix is a square matrix of order \( n \) in which the elements are mirrored across the main diagonal.

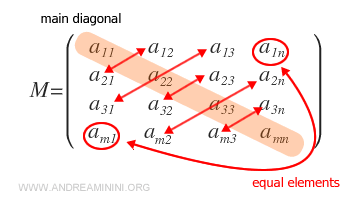
For a symmetric matrix, every element satisfies the condition \( a_{ij} = a_{ji} \) for all \( i, j = 1, ..., n \).

Note: Only square matrices can be symmetric. Matrices with different numbers of rows and columns ( \( m \neq n \) ) cannot be symmetric because their dimensions differ from those of their transpose. Additionally, only square matrices possess a main diagonal.

Symmetric matrices are commonly denoted by \( M^S \), where \( S \) stands for "symmetric."

The set of all symmetric matrices is also denoted as \( S(n, R) \), where \( n \) is the order of the matrix, and \( R \) represents the set of real numbers.

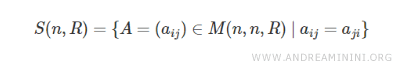
The set \( S(n, R) \) is a subset of the set of all square matrices with real coefficients, denoted \( M(n, n, R) \), where \( n \) is the matrix order.

A Practical Example

The matrix below has three rows ( \( m = 3 \) ) and three columns ( \( n = 3 \) ), making it a square matrix ( \( m = n \) ).

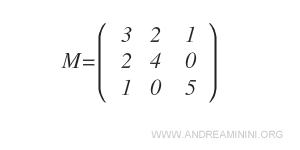
Since it is square, it has a well-defined main diagonal.

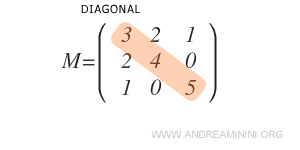
To check if it’s symmetric, we compare the elements in both the upper and lower triangular parts of the matrix.

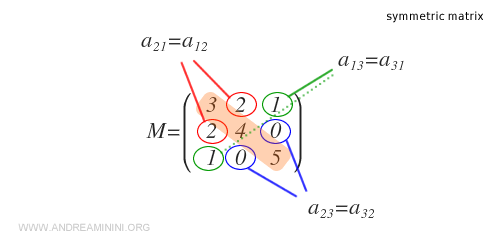
In this case, the matrix is symmetric because swapping the row and column indices does not alter the values of its elements.

Note: If a square matrix does not satisfy the symmetry condition, it is not symmetric.

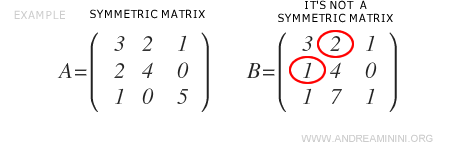
The Transpose of a Symmetric Matrix

A symmetric matrix \( M \) is always equal to its transpose \( M^T \).

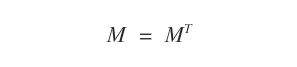
Example: The matrix \( M \) shown below is symmetric and therefore equals its transpose \( M^T \). When rows are swapped with columns, each element \( a_{ij} \) remains unchanged.

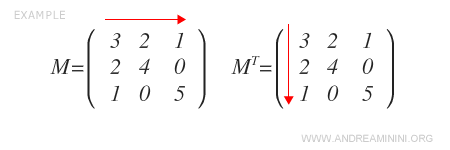
How to Calculate a Symmetric Matrix

Any square matrix of order \( n \) can be transformed into a symmetric matrix.

To calculate the symmetric form of a square matrix \( M \), the following formula is used:

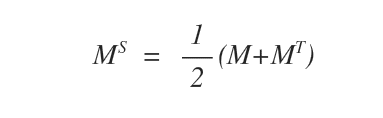
Another Practical Example

Here is a square matrix of order 3 that is not symmetric.

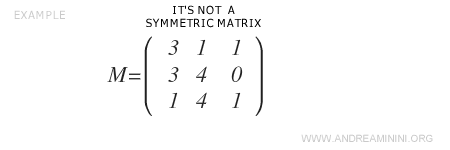
To transform \( M \) into a symmetric form, we first calculate its transpose \( M^T \).

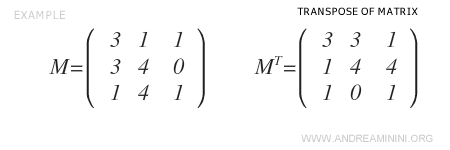
We then apply the formula \( \frac{1}{2} \cdot (M + M^T) \).

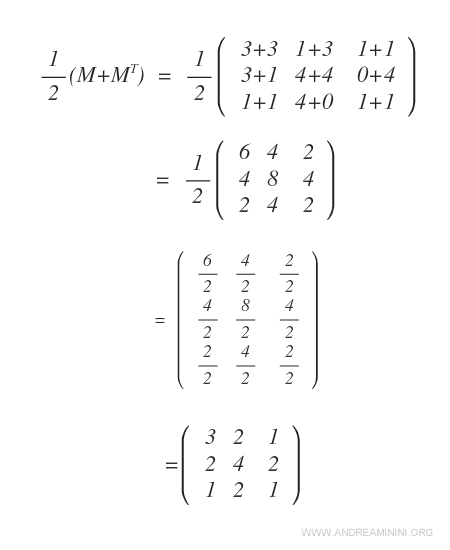
This process yields the symmetric matrix \( M_s \) derived from \( M \), with elements that are symmetric about the main diagonal.

Differences Between Symmetric and Antisymmetric Matrices

In a symmetric matrix, the condition \( a_{ij} = a_{ji} \) holds for all elements.

In contrast, an antisymmetric matrix has elements that satisfy \( a_{ij} = -a_{ji} \).

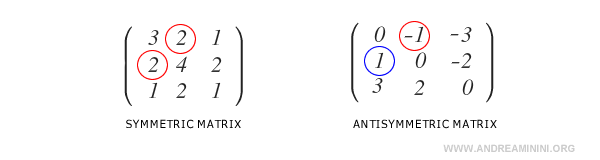
Note: A matrix that isn’t symmetric isn’t necessarily antisymmetric. The sets of symmetric matrices \( S_n(R) \) and antisymmetric matrices \( A_n(R) \) are distinct subsets within the space \( M_n(R) \) of matrices of order \( n \). These subsets intersect only at the zero matrix, which is both symmetric and antisymmetric.

Key Points on Symmetric Matrices

Some essential properties of symmetric matrices include:

1. All zero matrices are symmetric.
2. The sum of a symmetric matrix \( M^S \) and an antisymmetric matrix \( M^{AS} \) reconstructs the original matrix \( M \).
   
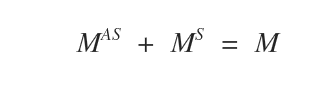
3. All diagonal matrices \( D(n, R) \) are symmetric matrices \( S(n, R) \).

   Proof: Diagonal matrices \( D(n, R) \) and symmetric matrices \( S(n, R) \) are both square matrices that share these characteristics:
   
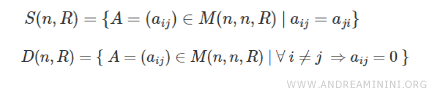
   In a diagonal matrix \( D(n, R) \), two cases arise:
   
   1) When \( i \neq j \), the element is zero ( \( a_{ij} = 0 \) ), so the elements at symmetric positions \( a_{ij} \) and \( a_{ji} \) are both zero, meeting the symmetry condition.
   
   2) When \( i = j \), \( a_{ij} \) and \( a_{ji} \) refer to the same element, naturally fulfilling the symmetry requirement.
   
   Therefore, all diagonal matrices \( D(n, R) \) are symmetric matrices \( S(n, R) \).