Complementary Minor in a Matrix

The complementary minor of an element a_ij in matrix A is the determinant of the square submatrix A_(ij), obtained by removing the i-th row and j-th column from A.

How to Calculate the Complementary Minor of an Element

To find the complementary minor of a_ij in matrix A, start by removing the i-th row and j-th column.

This produces the complementary submatrix A_(ij).

Next, calculate the determinant of A_(ij).

The determinant of A_(ij) is the complementary minor of a_ij.

Example Calculation

Consider this 3x3 square matrix A:

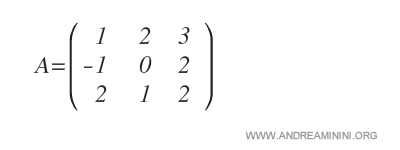
We’ll calculate the complementary minor of a₁₁.

To do this, remove the first row (i=1) and the first column (j=1).

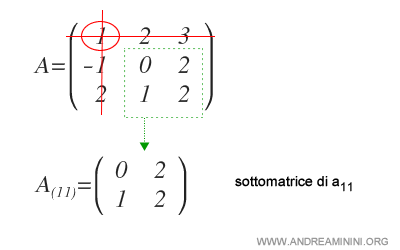
Now, find the determinant of submatrix A₍₁₁₎.

The determinant of A₍₁₁₎ is the complementary minor of a₁₁.

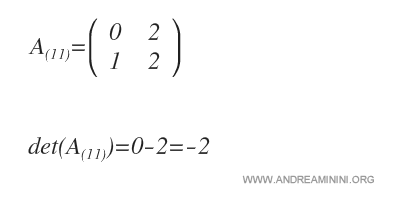
In this case, the complementary minor is 2.

Note: You can use this same method to find the complementary minors of other elements in matrix A.