Orthogonal Matrix

A matrix A is defined as orthogonal if its inverse, A^-1, is equal to its transpose, A^T.

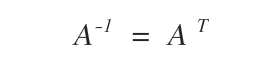
the Orthogonal matrix

The set of all n-dimensional orthogonal matrices is denoted by the symbol O_n.

Note. Only invertible matrices can be orthogonal, meaning orthogonal matrices form a subset of O_n within the set GL_n(R) of invertible n x n matrices.

In an orthogonal matrix, the product of matrix A with its transpose A^T equals the identity matrix I_n of order n.

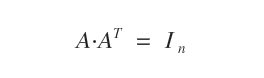
the corollary of orthogonal matrices

Proof

The proof is simple; one of the key properties of invertible matrices is as follows:

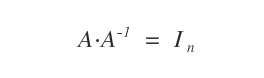
the property of invertible matrices

For orthogonal matrices, the inverse matrix is identical to the transpose, so A^-1 = A^T.

This leads to the conclusion that AA^T = I_n.

A practical example
The Orthogonal Matrix Groups O and SO

A practical example

The following square matrix is an orthogonal matrix.

example of orthogonal matrix

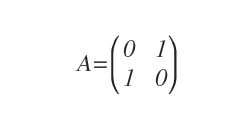
To confirm this, simply multiply A by its transpose, A^T.

The result of A · A^T is the identity matrix I₂.

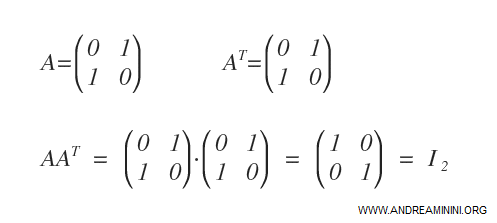
the product of a matrix and its transpose results in a unit matrix

Consequently, it follows that A^T = A^-1.

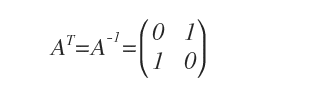
the transpose matrix is equal to the inverse matrix

Why? This is a property of inverse matrices: the product of an invertible matrix (A) with its inverse (A^-1) results in the identity matrix I. Therefore, if AA^T = I and AA^-1 = I, then A^T = A^-1.

This verifies that it is indeed an orthogonal matrix.

The Orthogonal Matrix Groups O and SO

All orthogonal matrices together form a mathematical structure known as the orthogonal group, denoted by $ O(n) $. These matrices satisfy the four fundamental axioms of abstract algebra that define a group:

Closure: the product of two orthogonal matrices is itself orthogonal;
Associativity: matrix multiplication is associative;
Identity element: the identity matrix $ I $ belongs to $ O(n) $ and serves as the neutral element;
Inverse element: every orthogonal matrix $ A $ has an inverse given by its transpose $ A^{T} $, which is also orthogonal.

Thus, the set of all real matrices $ A $ satisfying

$$ A^{T}A = AA^{T} = I $$

forms a group under matrix multiplication.

The orthogonal group $ O(n) $ represents all linear isometries of Euclidean space, that is, transformations that preserve both lengths and angles. Examples include rotations and reflections.

Note. In two dimensions, an orthogonal matrix in the group $ O(2) $ can represent either a rotation or a reflection of the plane. In three dimensions, the matrices in $ O(3) $ describe all spatial rotations and symmetries, which are transformations that leave the geometric structure of three-dimensional space unchanged.

Therefore, the group O(n) encompasses every possible rotation and reflection in an n-dimensional space.

However, not all of these transformations preserve orientation, since reflections reverse it.

For this reason, a particularly important subgroup is defined within $ O(n) $, known as the special orthogonal group $ SO(n) $, consisting of all orthogonal matrices with determinant equal to +1:

$$ SO(n) = \{ A \in O(n) \;|\; \det(A) = +1 \} $$

Matrices in $ SO(n) $ represent pure rotations, meaning transformations that preserve not only distances and angles but also the orientation of space.

Those with determinant -1 correspond to reflections, which reverse orientation.

Note. This distinction is fundamental in both geometry and physics. For instance, the group $ SO(3) $ describes all possible rotations in three-dimensional space, while $ SO(2) $ describes rotations in the plane.

And so on.