Multiplying matrices by scalars

When a matrix B is multiplied by a scalar α, the resulting matrix, denoted B', has each element b_ij scaled by α, meaning B'_ij = α·b_ij.

$$ \alpha \cdot B = ( \alpha \cdot b_{ij} ) $$

Practical Example: Here, we multiply the scalar α=3 by a matrix A. The result is matrix A, with each element scaled by three.

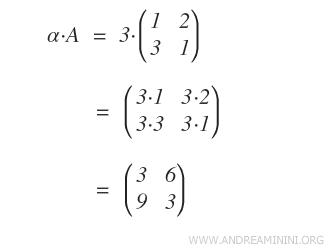
Properties of Scalar Multiplication

Scalar multiplication of a real number and a matrix follows these properties:

1. Distributive Property for Matrix Addition
   The product α·(A + B) equals the sum α·A + α·B.

   Note: Here, A and B are matrices, and α is a real number.

2. Distributive Property for Scalar Addition
   The product (α+β)·A is equivalent to the sum α·A + β·A.
3. Associative Property
   The product (α·β)·A is equal to α·(β·A).
4. Multiplicative Identity
   Multiplying a matrix by one leaves it unchanged: 1·A = A. Hence, one acts as the multiplicative identity.
5. Zero Property
   Multiplying any matrix by zero results in a zero matrix (0·A = O).
6. Multiplicative Inverse
   The product of -1 and matrix A gives the additive inverse, so (-1)·A = -A.