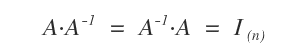Matrix multiplication

How do you multiply two matrices? In linear algebra, matrix multiplication is done through row-by-column multiplication, meaning each row in the first matrix is multiplied by each column in the second matrix.

For a real matrix A_mxn and a real matrix B_nxp, their product is a real matrix C_mxp. Each element c_ik in C is the sum of the products of corresponding elements from row i of A and column k of B.

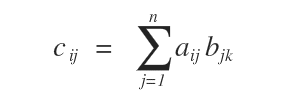
Matrix multiplication is defined only if the number of columns in the first matrix matches the number of rows in the second matrix.

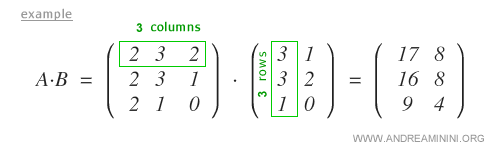
Note: Simply put, for matrix multiplication to be possible, each row in matrix A must contain the same number of elements as each column in matrix B. Un esempio pratico.

An Example of Matrix Multiplication

For example, let’s calculate the product of matrices A and B.

Matrix A is a 4x2 matrix, while matrix B is a 2x4 matrix.

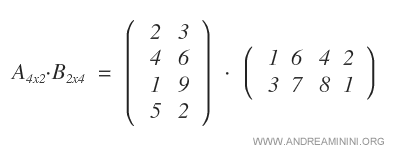
Since the number of columns in A matches the number of rows in B, we can proceed with the multiplication.

Note: The resulting matrix is a 4x4 matrix, created by multiplying the four rows of A (i=4) by the four columns of B (k=4).

We start by multiplying each row of matrix A by the first column of matrix B, resulting in the first column of the product matrix.

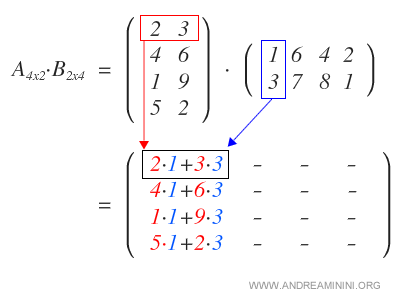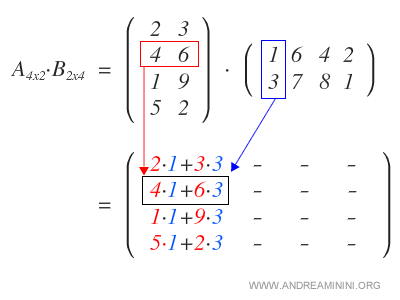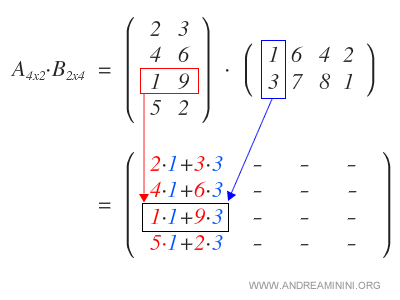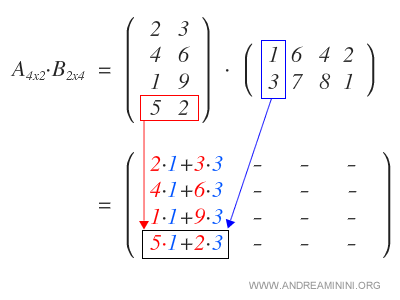
Next, we multiply the rows of A by the second column of B to form the second column of the resulting matrix.

This process continues with the third column, where rows of A are multiplied by the third column of B.

Finally, we multiply the rows of A by the fourth column of B to obtain the last column of the product matrix.

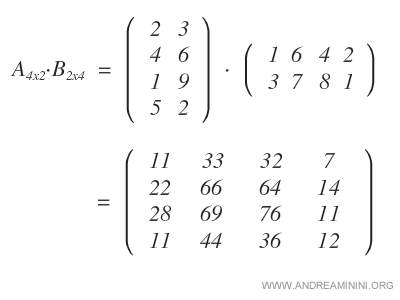
At this point, we have the final product matrix A·B.

Properties of Matrix Multiplication

Matrix multiplication has several important properties:

1. Associative Property: For any matrices A∈M_mn, B∈M_np, and C∈M_pq, the product A(BC) is the same as (AB)C.
   
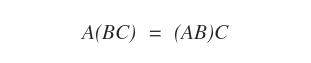
2. Right Distributive Property: For matrices A∈M_mn, B∈M_np, and C∈M_np, the product A(B+C) is equal to AB + AC.
   
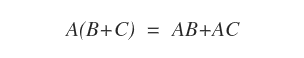
3. Left Distributive Property: For matrices A∈M_mn, B∈M_np, and C∈M_np, (A+B)C equals AC + BC.
   
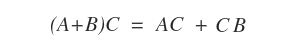
4. Scalar Multiplication: For any real number α∈R and matrices A∈M_mn and B∈M_np, α(AB) is the same as (αA)B or A(αB).
   
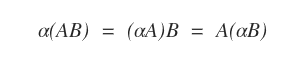
5. Transpose Property: For matrices A∈M_mn and B∈M_np, the transpose of (AB)^T is B^TA^T.
   
   

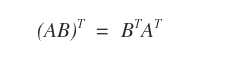
   Note: When transposing a matrix product, the order of matrices reverses; A is first in AB, but B^T is first in B^TA^T.

Key Differences Between Matrices and Real Numbers

Matrix Multiplication is Not Commutative

In general, A·B does not equal B·A.

This non-commutativity is due to the fact that switching the order of multiplication often produces matrices with different dimensions.

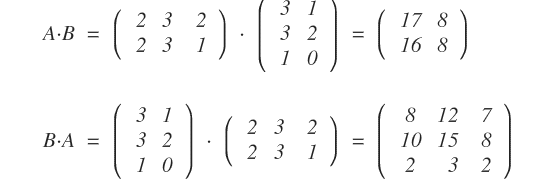
Note: While it’s rare, A·B can equal B·A if, for instance, one matrix is an identity matrix. However, this is the exception, not the rule.

In some cases, the reverse product doesn’t exist at all.

For example, matrix A may have the same number of columns as the rows of matrix B, but B may have more columns than A has rows.

In this case, A·B is defined, but B·A is not.

Matrix Multiplication Lacks the Cancellation Property

In matrix multiplication, you cannot cancel out matrices as you would with real numbers.

If A is multiplied by a zero matrix B, the result is a zero matrix.

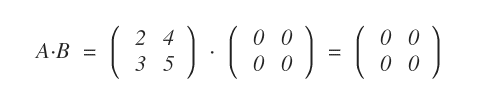
Interestingly, multiplying two non-zero matrices can also produce a zero matrix.

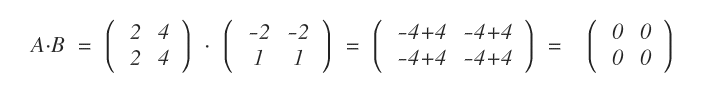
Thus, matrix multiplication does not obey the cancellation rule.

Matrices and the Multiplicative Inverse

In the realm of real numbers, any non-zero number x has a reciprocal, 1/x, such that x * (1/x) = 1.

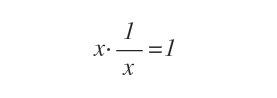
Matrices, however, do not always have this property. Only certain matrices, called invertible matrices, have an inverse, denoted A^-1, such that A * A^-1 equals the identity matrix I.

Note: Only invertible matrices have an inverse that, when multiplied by the original matrix, produces the identity matrix.