Upper Triangular Matrix

A square matrix is called an upper triangular matrix if all the elements below the main diagonal are zero: $$ \forall \ i > j \ \ \ \ a_{ij } = 0 $$

A Practical Example

Here’s an example of a 3×3 upper triangular matrix, with three rows and three columns.

Notice that all the elements below the main diagonal are zero.

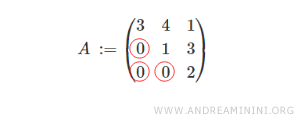
Note: The other elements of the matrix don’t have to be nonzero—they can be zero as well.

If the main diagonal is entirely composed of zeros, the upper triangular matrix is known as a strictly upper triangular matrix.

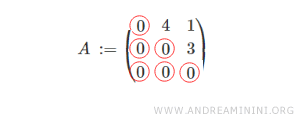
The set of upper triangular matrices with real coefficients of order \( n \) is denoted by \( T^R \).

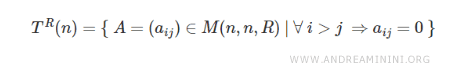
Why Are Upper Triangular Matrices Useful?

Upper triangular matrices are particularly useful because they simplify computations. Since all the relevant data is concentrated in just one part of the matrix, calculations become more efficient.

Additionally, the determinant of an upper triangular matrix is simply the product of the elements on the main diagonal, as all other terms contribute zero.

And so on.