Determinant Properties

The determinant of a matrix satisfies the following properties:

1. The determinant of a transposed matrix, det(A^T), is the same as the determinant of the original matrix, det(A).
   

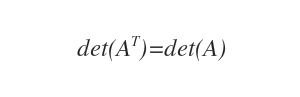
   Example. In the matrix below, transposing it does not affect the determinant.
   

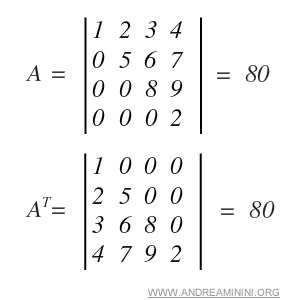
2. If a matrix is upper or lower triangular, its determinant is simply the product of the elements along the main diagonal.
   

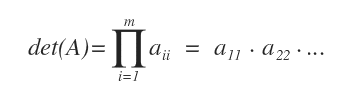
   Example. In these cases, computing the determinant is significantly faster.
   

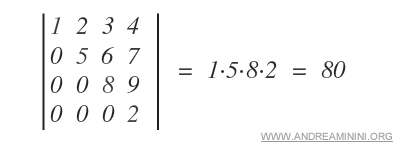
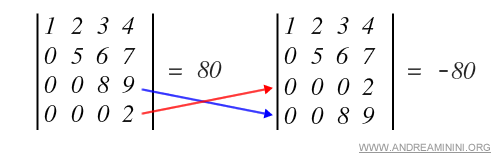
3. Swapping two rows or two columns flips the sign of the determinant.

   Example.
   

4. Multiplying a row or a column by a scalar \( \alpha \) scales the determinant by the same factor: det(\(\alpha\)A) = \(\alpha\) det(A).
   

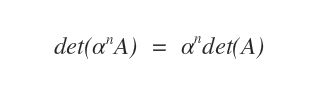
   Example. Here, the fourth row R₄ is multiplied by 2, which also doubles the determinant.
   

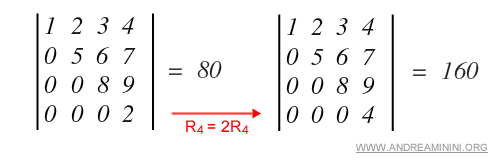
5. Adding a multiple of one row to another (or a multiple of one column to another) does not change the determinant.

   Example. In this case, the fourth row R₄ is updated by adding twice the first row R₁.
   

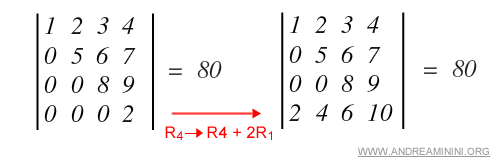
6. The determinant of a matrix is zero in the following cases:
   
   a) A row or a column consists entirely of zeros.
   
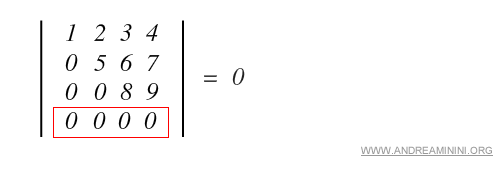
   b) Two rows or two columns are identical.
   
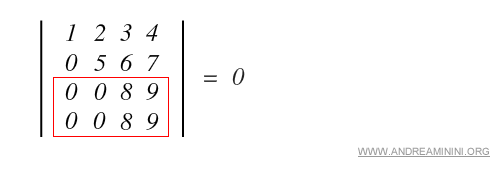
   c) Two rows or two columns are proportional.
   

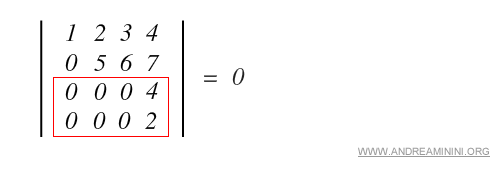
   Note. If a row or column can be expressed as a linear combination of other rows or columns, the matrix is linearly dependent, meaning its determinant is zero.

7. The determinant of the product of two matrices satisfies the following identity: det(AB) = det(A) det(B) ( Binet's Theorem ).
   
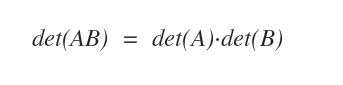
8. The determinant of the inverse of a matrix is the reciprocal of its determinant: det(A^-1) = 1/det(A).
   

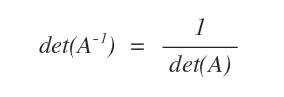
   Proof. According to Binet's theorem, the determinant of a product A·B is the product of their determinants: $$ det(A \cdot B) = det(A) \cdot det(B) $$ Applying this to an invertible matrix A and its inverse A^-1: $$ det(A \cdot A^{-1}) = det(A^{-1}) \cdot det(A) $$ Since multiplying a matrix by its inverse gives the identity matrix, we have: $$ det(A \cdot A^{-1}) = det(I) $$ The determinant of the identity matrix is 1, so: $$ det(A) \cdot det(A^{-1}) = 1 $$ Therefore: $$ det(A^{-1}) = \frac{1}{det(A)} $$ This completes the proof.

And so on.