Generators of a Vector Space

A generating system is a set of vectors S={v₁,...,v_m} in a vector space V $$ S = \{ v_1 , ... , v_m \} \in \ V $$ that allows for the determination of every vector v_i∈V in the vector space through the linear combination of the vectors in S with corresponding a₁,...a_m ∈ R scalar coefficients $$ \vec{v}_i=a_1 \vec{v}_1 +...+ a_m \vec{v}_m \ \ \ \forall v_i \in V $$

In essence, the linear combinations of the vectors S={v₁,...,v_m} generate all the vectors in the vector space V.

This is why the vectors in S are known as generators.

Therefore, given a set S of vectors in the vector space V

$$ S = \{ v_1, v_2, ... ,v_n \} $$

The smallest linear vector subspace L(S) that contains S is equal to the vector space V.

$$ L(S) = V $$

The number of generating vectors in S can be either finite or infinite, as long as it is always less than or equal to the number of vectors in the vector space V.

$$ m \le i $$

In these notes, I denote the set of generating vectors as S and the vector subspace of S as L(S).

The Purpose of a Vector Space Generator

A vector space V can consist of an infinite number of vectors. However, it's not necessary to list them all to describe it.

Every vector v ∈ V can be expressed as a linear combination of other vectors in the vector space.

Example

$$ v_4 = a_1 v_1 + a_2 v_2 + a_3 v_3 $$ $$ v_5 = a_1 v_1 + a_2 v_2 + a_3 v_3 $$ $$ v_6 = a_1 v_1 + a_2 v_2 + a_3 v_3 $$ $$ \vdots $$

It's sufficient to choose a suitable finite or infinite subset of vectors S={v₁,..,v_m}.

$$ L = \{ v_1 , v_2 , v_3 \} $$

Through the linear combination of the vectors in S with m scalar numbers α_m, any other vector in the vector space V can be obtained.

$$ \forall \ v_i \in V \: \: v = a_1 v_1 + a_2 v_2 + a_3 v_3 $$

An Example of a Vector Space Generator

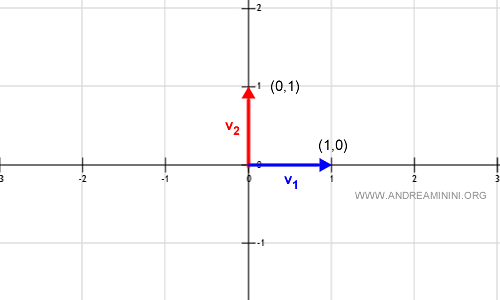
The entire vector space V = R² over the field of real numbers R can be generated by just two vectors.

$$ v_1 = ( 1, 0 ) $$ $$ v_2 = ( 0, 1 ) $$

On the Cartesian plane R², these two vectors are represented as follows:

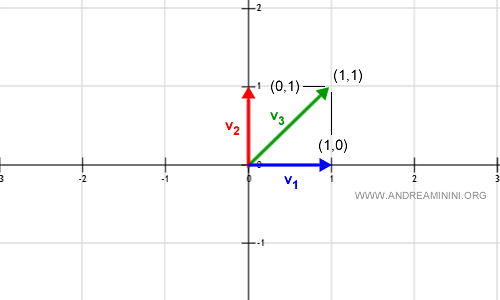
To demonstrate that vectors v₁ and v₂ are generators of the vector space R², I write their linear combination with two scalars a₁ and a₂ belonging to R.

$$ v = a_1 v_1 + a_2 v_2 \: \: \: \: \: \: with \: \: a_1=1 , a_2=1 $$

$$ v = 1 ( 1 , 0 ) + 1 ( 0 , 1 ) = $$

$$ v = ( 1 , 0 ) + ( 0 , 1 ) $$

$$ v = ( 1 , 1 ) $$

This linear combination generates another vector (v₃) in the vector space V, pointing to the coordinates (1,1).

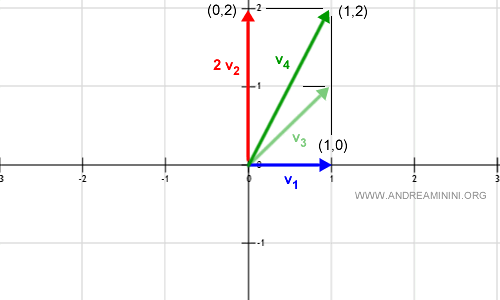
Now, I modify the linear combination using the scalar a₂=2.

$$ v = a_1 v_1 + a_2 v_2 \: \: \: \: \: \: with \: \: a_1=1 , a_2=2 $$

$$ v = 1 ( 1 , 0 ) + 2 ( 0 , 1 ) = $$

$$ v = ( 1 , 0 ) + ( 0 , 2 ) $$

$$ v = ( 1 , 2 ) $$

Here, vector v₂ has doubled in length while v₁ remains unchanged.

This linear combination generates another distinct vector (v₄) in the vector space, pointing to the coordinates (1,2).

In this way, by altering the scalars a₁ and a₂ for vectors v₁ and v₂, I can generate every vector v in the vector space V.

Therefore, I can assert that v₁ and v₂ form a generating system for the vector space R².

$$ L_R = \{ v_1 , v_2 \} = R^2$$

And so on.

Note. A single vector v₁ alone is not a generator of the vector space V=R² as it only generates vectors along the x-axis. It is merely a generator of the subspace {x}. Similarly, vector v₂, taken individually, does not generate R² as it only produces vectors along the y-axis, thus being a generator of the subspace {y}.

Example 2

A vector space generator can also consist of just one vector.

For instance, in a vector space V over the field K=R of real numbers, consider any non-zero vector v.

$$ \vec{v} \in V $$

Visually speaking

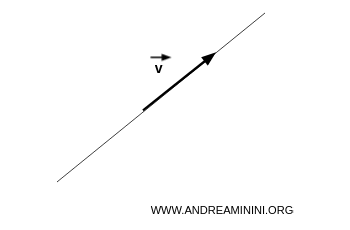
The vector v must be non-zero.

$$ \vec{v} \in \vec{0} $$

The set generated by vector L(v) comprises the linear combination of vector v with scalars k from K

$$ L(v) = \{ k \cdot \vec{v} \} $$

The vectors generated share the same direction as the generating vector, meaning they lie on the same line.

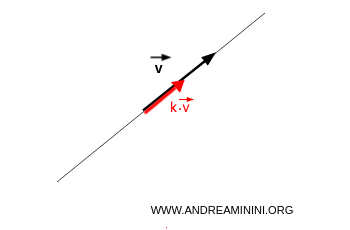
What varies is the direction and magnitude (length) of each vector.

Note. The generating vector must be non-zero, because any scalar multiplied by a magnitude of zero always results in zero.

Example 3

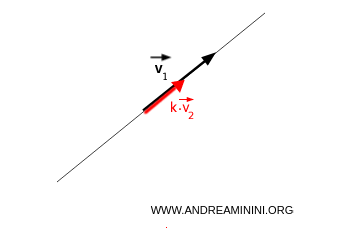
Generally, two non-zero vectors v₁, v₂ generate a vector subspace

$$ \vec{v_1} \ne 0 $$ $$ \vec{v_2} \ne 0 $$

The subspace generated depends on the linear dependence or independence between the two vectors.

• If the two vectors are parallel $$ \vec{v_1} = k \cdot \vec{v_2} $$, then the vector subspace generated by the two vectors L(v₁,v₂) lies on the line containing the two vectors v₁, v₂.
  
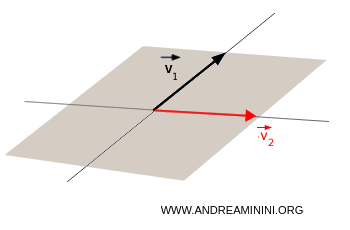
• If the vectors are not parallel $$ \vec{v_1} \ne k \cdot \vec{v_2} $$, then the vector subspace generated by the two vectors is the plane containing both vectors v₁ and v₂.
  

How to Determine if Vectors are Generators

To find out if a set of vectors forms a generating system for the vector space V, we need to solve the equation system representing their linear combination.

A Practical Example

Consider two vectors v₁=(1,0) and v₂=(2,1) in the vector space V=R².

$$ v_1 = (1,1) $$ $$ v_2 = (2,1) $$

Our goal is to determine if these vectors are generators of the vector space V.

The linear combination of vectors v₁ and v₂ can be expressed as:

$$ a_1 v_1 + a_2 v_2 $$

$$ a_1 (1,1) + a_2 (2,1) $$

$$ ( a_1 , a_1 ) + (2 a_2 , a_2 ) $$

$$ ( a_1 + 2 a_2 , a_1 + a_2 ) $$

These last two expressions represent the target coordinates (x,y) of the vector generated by the linear combination of the two vectors.

$$ (x,y) = ( a_1 + 2 a_2 , a_1 + a_2 ) $$

We can rewrite this vector equality as a system of equations:

$$ \begin{cases} a_1 + 2 a_2 = x \\ a_1 + a_2 = y \end{cases}$$

If this system has solutions for a₁ and a₂ for every possible value of (x,y), then vectors v₁ and v₂ are indeed generators of the vector space V=R².

Conversely, if there are no solutions, then these vectors are not generators of V=R².

 

Note. To demonstrate that the system has solutions (either one or infinitely many), we can apply the Rouché-Capelli theorem. According to this theorem, a system of linear equations has solutions if the rank of the coefficient matrix A is equal to the rank of the augmented matrix A|B. In such cases, the system has ∞^n-r solutions, where r is the rank and n is the number of unknown variables.

In this case, the system has solutions.

Therefore, v₁ and v₂ are generators of the vector space R².

Verification

As an additional check, let's compute the solutions of the system.

$$ \begin{cases} a_1 + 2 a_2 = x \\ a_1 = y - a_2 \end{cases}$$

$$ \begin{cases} y - a_2 + 2 a_2 = x \\ a_1 = y - a_2 \end{cases}$$

$$ \begin{cases} y + a_2 = x \\ a_1 = y - a_2 \end{cases}$$

$$ \begin{cases} a_2 = x - y \\ a_1 = y - a_2 \end{cases}$$

$$ \begin{cases} a_2 = x - y \\ a_1 = y - (x-y) \end{cases}$$

$$ \begin{cases} a_2 = x - y \\ a_1 = 2y - x \end{cases}$$

These equations are solved for any combination of x and y values, i.e., over all points on the Cartesian plane.

Thus, v₁ and v₂ are indeed generators of the vector space R².

Difference Between a Set of Generators and Linear Span

A linear span is a set of vectors S_p in the vector space V

$$ S_p = \{ v_1,.v_2, ...,v_m \} $$

whose linear combination is a vector in V.

$$ a_1 v_1 + ... + a_m v_m \in V $$

Every linear combination of the vectors in the span S_p belongs to the vector space V.

$$ L(S_p) \subseteq V $$

However, it does not imply that every vector in the vector space V can be obtained through a linear combination of the span set S_p.

$$ L(S_p) \ne V $$

Note. The vectors in the span {v₁,...,v_n} are certainly generators for a subspace L(S_p). It does not necessarily mean they are for the entire vector space V.

Conversely, a set of generators is a collection S of vectors

$$ S = \{ v_1,.v_2, ...,v_n \} $$

whose linear combination generates all vectors in the vector space V.

$$ L(S) = V $$

Therefore, a set of vectors forming a span is not necessarily a set of generators.

$$ L(S_p) \ne L(S) = V $$

How to Minimize a Set of Generators

A set of vectors {v₁,...,v_m} forms a generating system, but it's not necessarily the smallest possible set of generators for the vector space V.

Indeed, consider a generating system:

$$ v = a_1 v_1 + ... + a_m v_m $$

If you add another vector v_m+1 with a scalar a_m+1 = 0, you end up with another generating system for the same vector space V.

$$ v = a_1 v_1 + ... + a_m v_m + a_{m+1} v_{m+1} $$

$$ with \:\:\: a_{m+1} = 0 $$

Therefore, even though a set of vectors is a generating system for the vector space, it can potentially be further reduced.

Example

How Do You Reduce a Set of Generators?

To reduce a set of generators, one must eliminate the vectors linearly dependent on others.

Demonstration

In a set of generators, the vector v_m is linearly dependent on the others.

$$ v = a_1 v_1 + ... + a_m v_m $$

Hence, v_m can be rewritten as a linear combination of the other vectors.

$$ v = β _1 v_1 + ... + β _{m-1} v_{m-1} $$

Substituting this linear combination into the generating system:

$$ v = a_1 v_1 + ... + a_m ( β _1 v_1 + ... + β _{m-1} v_{m-1} ) $$

$$ v = a_1 v_1 + ... + a_m β _1 v_1 + ... + a_m β _{m-1} v_{m-1} ) $$

$$ v = v_1 ( a_1 + a_m β _1 ) + ... + v_{m-1} ( a_{m-1} + a_m β _{m-1} ) $$

The coefficients (a₁+a_mβ₁ ) ... (a_m-1+a_mβ_m-1 ) are still scalar numbers from the field R.

So, they can be rewritten as γ₁ , ... , γ_{m-1 ∈} R

$$ v = γ _1 v_1 + ... + γ _{m-1} v_{m-1} $$

This shows that even { v₁, v₂ } can be a generating system for the vector space V.

And so on.

Example

Difference Between a Set of Generators and a Basis

A set of generators is called a basis of the vector space V if the vectors in the set S $$ S = \{ v_1, v_2, ... , v_n \} $$ are linearly independent.

A basis is also known as a free system of generators.

The linear combinations of vectors in the set S={v₁,v₂,..,v_n} generate all vectors in the vector space V.

$$ \vec{v}_i=a_1 \vec{v}_1 +...+ a_m \vec{v}_n \ \ \ \forall \ v_i \in V $$

The same holds true in generating systems.

However, in the case of a basis, each vector in the vector space V is generated by one and only one linear combination of the vectors in set S.

Note. Conversely, in a generating system with linearly dependent vectors, any vector in the vector space V can be composed of infinite combinations of vectors in set S.

In these cases, the generating system is called a basis of the vector space.