Vector Subspace Generated by a Set of Vectors

The vector subspace generated by a set S of vectors in the vector space V $$ S = \{ v_1 , v_2, ... , v_n \} $$ is the smallest vector subspace of V that includes S. It is denoted by L(S) or <S>. $$ L(S) \ \ \ or \ \ \ <S> $$ Here, L stands for linear.

The set of vectors S is not a subspace itself.

$$ S = \{ v_1 , v_2, ... , v_n \} $$

The subspace L(S) consists of all vector combinations from the set S

$$ L(S) = \{ \lambda_1 v_1 + \lambda_2 v_2 + ... + \lambda_n v_n \ | \ v_i \in S \ , \ \lambda_i \in K \} $$

The Explanation

Consider a vector space V.

Take a set S of vectors from the vector space V.

$$ S = \{ v_1 , v_2, ... , v_n \} \subset V $$

By assumption, the set S is not a vector space. It's merely a set composed of 2 or more vectors.

The smallest vector subspace of V that contains the set S is known as the vector subspace generated by the set S of vectors and is represented by the symbol L(S) or <S>

$$ L(S) \ \ \ or \ \ \ <S> $$

The vector subspace L(S) is formed by the linear combination of the n vectors of S with an equal number of n scalars k.

$$ L(S) = \{ k_1 \vec{v}_1 + k_2 \vec{v}_2 + ... + k_n \vec{v}_n \ \ | \ \ v_i \in S \ . \ k_i \in K \} $$

This can also be expressed using a summation

$$ L(S) =\{ \sum_{i=1}^n k_i \vec{v}_i \ | \ \vec{v}_i \in S \} $$

The vector subspace L(S) is composed of m≥n vectors obtained from the linear combination of the n vectors in the set S.

Subspace Generated by a Single Vector

Consider a single non-zero vector in the vector space

$$ \vec{v} \in V \ , \ \vec{v} \ne 0 $$

Hence, the set S consists of just one vector

$$ S = \{ \vec{v} \} \subset V $$

Geometrically, the vector lies on a line.

In this case, the subspace generated by S is the set L(S) of vectors resulting from the linear combination of a single vector with a scalar

$$ L(\vec{v}) = \{ \lambda \vec{v} \ | \ \forall \ \lambda \in K \} $$

The vector subspace consists of all vectors that lie on the same line.

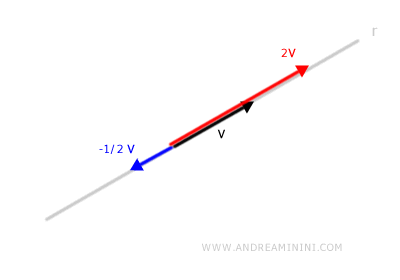
The vectors in the subspace all share the same direction.

However, they can vary in length and orientation.

Note. In the special case where the vector is the zero vector, the vector subspace generated by the zero vector consists only of the zero vector itself. $$ L(\vec{0}) = \{ \vec{0} \} $$ because the product of a scalar and the zero vector is always the zero vector.

 

Subspace Generated by Two Vectors

The subspace generated by two non-zero vectors v₁, v₂ in the vector space V over the field K

$$ v_1, v_2 \in V \ , \ v_1,v_2 \ne \vec{0} $$

depends on whether these two vectors are linearly dependent or independent.

• If the two vectors are parallel
  Here, the vectors are linearly dependent. One vector can be written as a multiple of the other. $$ \vec{v}_1 = \lambda \cdot \vec{v}_2 \ \ \alpha \in K $$ The two vectors share the same direction and lie on the same line.
  
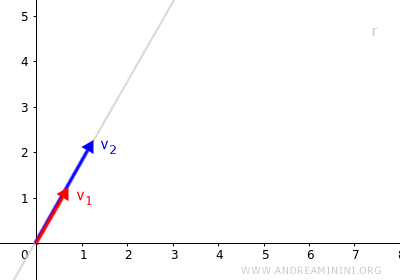
  Hence, the linear combinations of these two vectors are vectors that reside on the same line as v₁ and v₂. $$ L(\vec{v}_1 , \vec{v}_2) = \{ \lambda_1 \vec{v}_1 + \lambda_2 \vec{v}_2 \ | \ \forall \ \lambda \in K \} $$
• If the two vectors are not parallel
  In this scenario, the vectors are linearly independent. One vector cannot be written as a multiple of the other. $$ \vec{v}_1 \ne \lambda \cdot \vec{v}_2 \ \ \alpha \in K $$ These vectors have different directions, meaning they lie on separate lines.
  
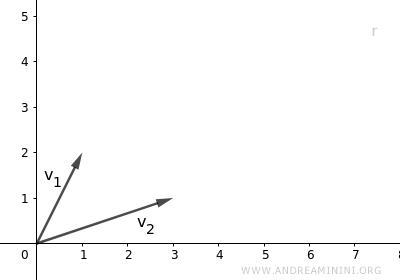
  Therefore, the linear combinations of these two vectors are vectors that reside in the same plane containing v₁ and v₂. $$ L(\vec{v}_1 , \vec{v}_2) = \{ \lambda_1 \vec{v}_1 + \lambda_2 \vec{v}_2 \ | \ \forall \ \lambda \in K \} $$

Example

Let's consider the set of vectors

$$ S = \{ v_1, v_2 \} $$

The vectors v₁ and v₂ are

$$ v_1 = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

Geometrically, these two vectors are linearly independent in the plane as they are not parallel.

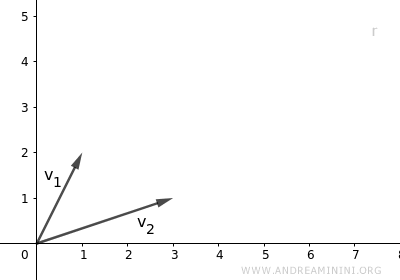
The set of vectors belongs to the vector space V=R²

$$ S \subset V=R^2 $$

The set L(S) is the smallest vector subspace generated by the two vectors v₁ and v₂, or their linear combinations

$$ L(S) = \lambda_1 \cdot \vec{v}_1 + \lambda_2 \vec{v}_2 $$

$$ L(S) = \lambda_1 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

Where λ₁ and λ₂ are any real coefficients.

The vector subspace L(S) consists of all vectors generated by the linear combinations of vectors v₁ and v₂.

Note. By taking λ₁=2 and λ₂=3, the linear combination yields the vector v_n=(11,7) $$ \vec{v}_n= \lambda_1 \cdot \vec{v}_1 + \lambda_2 \vec{v}_2 $$ $$ \vec{v}_n = 2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} + 3 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 2 \cdot 1 \\ 2 \cdot 2 \end{pmatrix} + \begin{pmatrix} 3 \cdot 3 \\ 3 \cdot 1 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 9 \\ 3 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 2+9 \\ 4+3 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 11 \\ 7 \end{pmatrix} $$ From a geometric standpoint

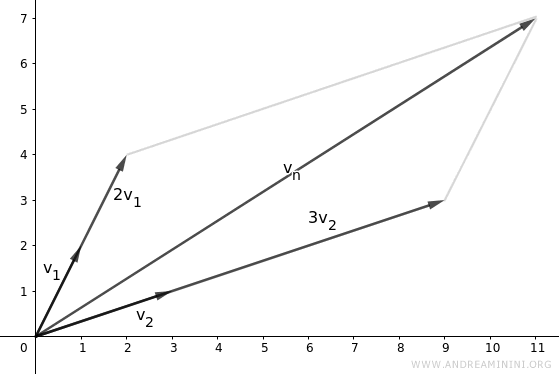
And so on.