Direct Sum of Vector Subspaces
The sum of two subspaces A and B is called a direct sum, if their intersection A⋂B consists only of the zero vector.
Given a vector space V over the field K, with A and B as two subspaces of V, if A⋂B = {0v}, then the sum is called direct. $$ A \oplus B $$
The direct sum is denoted by a + symbol inside a circle.
Practical Examples
Here are two practical examples to calculate and verify the existence or absence of a direct sum between two or more vector subspaces.
Example 1
In a vector space V within the R3 field, consider these two vector subspaces A and B.
$$ A = \{ (x,y,z) \in R^3 , \begin{cases} x=0 \\ y=0 \end{cases} \} $$
$$ B = \{ (x,y,z) \in R^3 , z=0 \} $$
Subspace A corresponds to the z-axis (blue) in the three-dimensional space.
Subspace B, on the other hand, is the (x,y) plane in the three-dimensional space at z=0 (red plane).
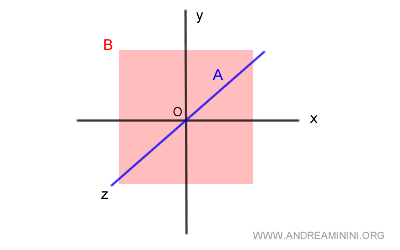
If subspaces A and B are in direct sum, the intersection A⋂B comprises only the null vector 0v.
$$ A \cap B=\{0_v\} $$
In this case, it is true. The set A⋂B includes only the trivial intersection (origin O).
Therefore, the subspaces A and B are in direct sum with each other.
$$ A \oplus B $$
Example 2
In a vector space V within the R3 field, consider two vector subspaces A and B.
$$ A = \{ (x,y,z) \in R^3 , \begin{cases} x=0 \\ y=0 \end{cases} \} $$
$$ C = \{ (x,y,z) \in R^3 , y=0 \} $$
Subspace A corresponds to the z-axis (blue) in the three-dimensional space.
Subspace C, however, is the (x,z) plane in the three-dimensional space at y=0 (red plane).
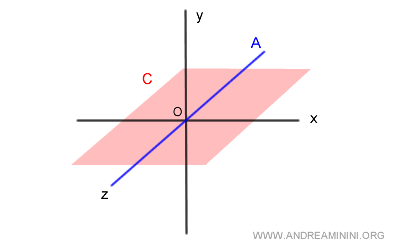
To verify the direct sum, calculate the intersection between A and C
$$ A \cap C=\{ R \} <> \{ 0_v \}$$
The intersection set A⋂B consists of the infinite points on the Z-axis (blue). It's different from { 0v }.
Therefore, in this case, the subspaces A and C are not in direct sum with each other.
And so on.
