Sum of Vector Subspaces

Given a vector space V over the field K, and two subspaces A and B of V, the sum A+B of the subspaces is a vector subspace formed by the sum of vectors from A and B. $$ A+B := \{ \vec{a}+\vec{b}, \vec{a} \in A, \vec{b} \in B \} $$ Thus, the sum of the subspaces encompasses the union of the two subspaces $$ A∪B \subset A+B $$ Moreover, A+B is the smallest vector subspace containing the union of the subspaces A∪B.

The sum of two subspaces A+B is a subspace of the vector space V.

It is referred to as the sum subset of V.

$$ A+B \in V $$

Being a vector space, V inherits the sum properties of vector spaces.

In turn, the sum of the subspaces A+B includes both subspaces A and B.

$$ A \in A+B $$

$$ B \in A+B $$

Furthermore, the space A+B is the smallest vector subspace of V that contains both A and B as subspaces.

 

Note. The union A∪B is not a vector subspace because the union of subspaces is not itself a vector subspace.

Proof

The sum of the subspaces A+B is a vector subspace

First, I need to demonstrate that the sum of vector subspaces is a vector subspace.

It's important to note that the subspaces A and B include the zero vector 0.

Therefore, the set A+B also contains the zero vector.

$$ \vec{a} + \vec{b} = \vec{0} + \vec{0} = \vec{0} \in A+B $$

Now I can verify if it meets the two properties of vector subspaces.

1) Sum Property

Let's take two generic vectors u and w from A+B.

$$ \vec{u},\vec{w} \in A+B $$

Where u and w are vectors obtained by summing a vector from A with a vector from B

$$ \vec{u} = \vec{a_1} + \vec{b_1} $$

$$ \vec{w} = \vec{a_2} + \vec{b_2} $$

with

$$ \vec{a_1} \ , \ \vec{a_2} \in A $$

$$ \vec{b_1} \ , \ \vec{b_2} \in B $$

The sum of the vectors

$$ \vec{u} + \vec{w} = (\vec{a_1} + \vec{b_1} ) + (\vec{a_2} +\vec{b_2} ) $$

Can be rewritten, thanks to the associative property, as

$$ \vec{u} + \vec{w} = (\vec{a_1} + \vec{a_2} ) + ( \vec{b_1} + \vec{b_2} ) $$

The sum of the vectors a₁+a₂ is a sum vector belonging to the vector subspace A.

Similarly, the sum of the vectors b₁+b₂ is a sum vector of the subspace B.

$$ \vec{a_1} + \vec{a_2} \in A $$

$$ \vec{b_1}+\vec{b_2} \in B $$

The sum of a vector from A with a vector from B belongs to the set A+B

$$ \vec{u} + \vec{w} = ( \vec{a_1} + \vec{a_2} ) + ( \vec{b_1} + \vec{b_2}) \in A+B $$

Therefore, the set A+B is closed with respect to addition.

This is the first property of vector subspaces.

2) Scalar Multiplication Property

Given a scalar k from K and the sum u+w of two generic elements from A+B.

$$ k \in K $$

$$ \vec{u}+\vec{w} \in A+B $$

where u and w are vectors obtained by summing a vector from A with a vector from B

$$ \vec{u} = \vec{a_1} +\vec{b_1} $$

$$ \vec{w} = \vec{a_2} + \vec{b_2} $$

with

$$ \vec{a_1}, \vec{a_2} \in A $$

$$ \vec{b_1}, \vec{b_2} \in B $$

The scalar multiplication of k with the sum of elements

$$ k ( \vec{u} + \vec{w} ) = k ( \vec{a_1} + \vec{b_2} ) + k ( \vec{a_2} + \vec{b_2} ) $$

can be rewritten as

$$ k ( \vec{u} + \vec{w} ) = k \vec{a_1} + k \vec{b_1} + k \vec{a_2} + k \vec{b_2} $$

or

$$ k ( \vec{u} + \vec{w} ) = k ( \vec{a_1} + \vec{a_2} ) + k ( \vec{b_1} + \vec{b_2} ) $$

where

$$ k (\vec{a_1}+\vec{a_2}) \in A $$

$$ k (\vec{b_1}+\vec{b_2}) \in B $$

Thus

$$ k ( \vec{u} + \vec{w} ) \in A+B $$

The scalar product ka belongs to the set A+B.

Therefore, the set A+B is closed with respect to scalar multiplication.

This also satisfies the second property of vector subspaces.

Since both properties of vector subspaces are met, it follows that the sum of two vector subspaces is a vector subspace.

The sum of the subspaces A+B contains the union A∪B

Next, I need to prove that the sum of the subspaces A+B contains the union of the subspaces A∪B

Every vector from subspace A can be written as the sum of the vector with the zero vector

$$ \forall \vec{a} \in A \ \Rightarrow \vec{a} = \vec{a} + \vec{0} $$

Since the sum A+B is a vector subspace, it contains the zero vector.

Therefore, the subspace A is contained within the sum A+B of the subspaces

$$ A \subset A+B $$

The same logic applies to every vector from the subspace B

$$ \forall \vec{b} \in B \ \Rightarrow \vec{b} = \vec{b} + \vec{0} $$

Thus, the subspace B is also contained within the sum A+B of the subspaces

$$ B \subset A+B $$

In conclusion, the sum of the subspaces A+B includes all vectors from A and B, i.e., it contains the union of the subspaces A∪B.

$$ A \cup B \subset A+B $$

A Practical Example

Consider the vector space V=R³

$$ V = R^3 $$

and two vector subspaces

$$ A = \{ \vec{a} \in R, \vec{b}=0 \} $$

$$ B = \{ \vec{a} = 0, \vec{b} \in R \} $$

The subspace A consists of vectors along the x-axis.

The subspace B consists of vectors along the y-axis.

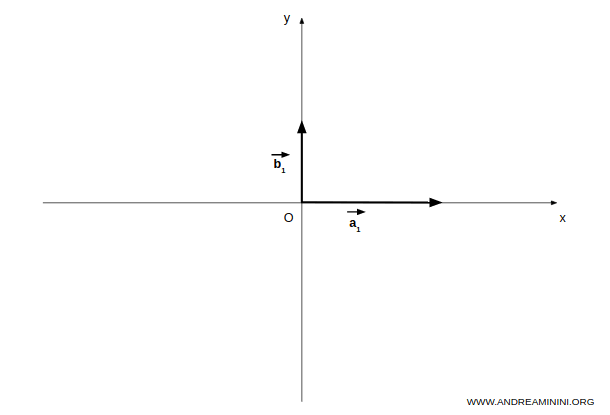
Now, consider the subspace formed by the sum of the vector subspaces A+B

$$ A+B $$

The sum subspace A+B encompasses both subspaces A and B.

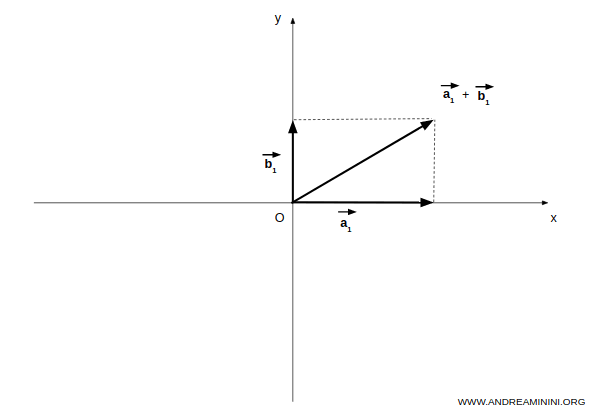
Moreover, as a subspace, it includes any vector sum and any scalar multiplication of a vector, effectively the entire plane.

The Smallest Subspace Containing A and B

The sum of vector spaces A+B is the smallest vector subspace of V that contains the union of the subspaces A∪B.

Proof

Consider any vector subspace L that contains all vectors of A and B, namely the union of the two subspaces A∪B.

$$ A \cup B \subseteq L $$

Hence, every vector from subspace A is also in L

$$ \forall \ a \in A \rightarrow a \in L $$

The same holds true for vectors from B

$$ \forall \ b \in B \rightarrow b \in L $$

As L is a vector subspace, by definition, it also contains the sum of vectors from A and B

$$ \{ \vec{a}+\vec{b} \ | \ \vec{a} \in A \ , \ \vec{b} \in B \} \subseteq L $$

Thus, the vector subspace L includes the vector subspace A+B

$$ A+B \subseteq L $$

In general, any vector subspace containing A and B also includes their sum A+B.

Therefore, among all vector subspaces that contain the union of subspaces A∪B, the sum subspace A+B is the smallest.

Note. The subspace of the sum of subspaces A+B is contained in all subspaces that contain A and B. Consequently, A+B is definitely the smallest among all subspaces containing A and B. Furthermore, any subset smaller than A+B that contains A and B, $$ A, B \subset Z \subset A+B $$, is not a subspace because it does not satisfy one of the properties of vector subspaces, as the sum of vectors from A and B is not an internal operation in Z. Therefore, A+B is the smallest subspace capable of containing the subspaces A and B.

And so on