Complementary Subspaces
Vector subspaces are called complementary subspaces if they form a direct sum and their sum equals the entire vector space.
Definition of Complementary Spaces
Given two subspaces A and B of the vector space V, they are complementary subspaces if
$$ \begin{cases} A \oplus B \\ A + B = V \end{cases} $$
The first property (direct sum) implies a trivial intersection.
$$A \oplus B => A \cap B = \{ 0_v \} $$
The second property states that the sum of the subspaces A+B equals the entire vector space V.
$$ A+B = V $$
When two subspaces are complementary, it is denoted as
$$A \oplus B = V $$
Both properties must be satisfied to define complementary spaces. One alone is not sufficient.
Difference between Direct Sum and Sum of Subspaces. The direct sum is the intersection set of the two subspaces consisting only of the null vector { 0v }. The sum of two subspaces, however, is the set formed by the sums of their elements.
Practical Examples
In these examples, I check whether two vector subspaces are complementary or not.
Example 1
Given a vector space V in the R3 field and two vector subspaces A and B.
$$ A = \{ (x,y,z) \in R^3 ,\begin{cases} x=0 \\ y=0 \end{cases} \} $$
$$ B = \{ (x,y,z) \in R^3 , z=0 \} $$
The subspace A is the z-axis (blue) in the 3-dimensional space.
The subspace B, on the other hand, is the (x,y) plane (red) in the 3-dimensional space at z=0.
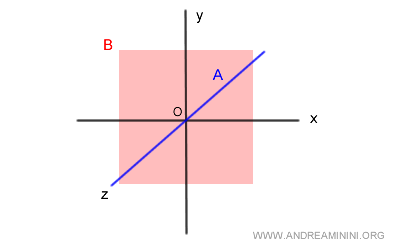
The intersection A∩B consists only of the null vector 0v (trivial intersection).
$$ A \cap B = \{0_v\} $$
Therefore, subspaces A and B are in direct sum with each other.
$$ A \oplus B $$
This is the first condition for complementary vector spaces.
Now I need to verify if the sum A+B equals the vector space V.
$$ A+B = V $$
The sum shifts the B plane to every point along the Z axis.
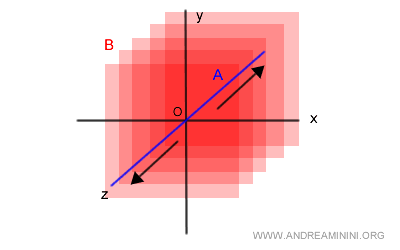
Thus, the sum A+B equals the vector space V in the R3 field.
The second condition for complementary spaces is also satisfied.
Therefore, the subspaces A and B are complementary subspaces.
Example 2
Given a vector space V in the R3 field and two vector subspaces A and B.
$$ A = \{ (x,y,z) \in R^3 ,\begin{cases} x=0 \\ y=0 \end{cases} \} $$
$$ B = \{ (x,y,z) \in R^3 ,\begin{cases} z=0 \\ y=0 \end{cases} \} $$
The subspace A is the z-axis (blue), while the subspace B is the x-axis (red) in the 3-dimensional space.
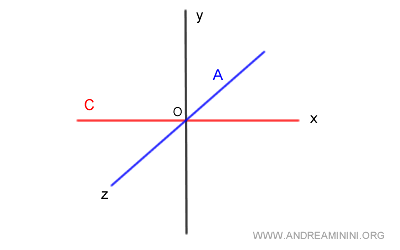
The intersection A∩B is trivial as it includes only the null vector 0v.
$$ A \cap B = \{0_v\} $$
Therefore, subspaces A and B are in direct sum with each other.
$$ A \oplus B $$
Now I must verify if their sum A+B equals the vector space V.
$$ A+B = \{ (x,y) \in R^2 \} $$
The sum A+B corresponds to the (x,z) plane in two dimensions (R2).
It does not correspond to the three-dimensional vector space V (R3).
Therefore, although in direct sum with each other, in this case the subspaces A and B are not complementary subspaces.
Example 3
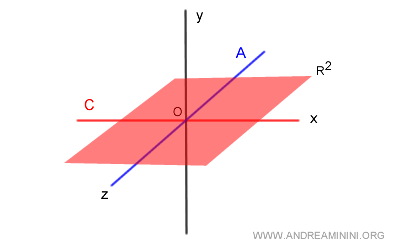
Given a vector space V in the R3 field, I take two vector subspaces A and B.
$$ A = \{ (x,y,z) \in R^3 , \begin{cases} x=0 \\ y=0 \end{cases} \} $$
$$ C = \{ (x,y,z) \in R^3 , y=0 \} $$
The subspace A is with the z-axis (blue) of the 3-dimensional space.
The subspace C, however, is the (x,z) plane of the 3-dimensional space at y=0 (red plane).
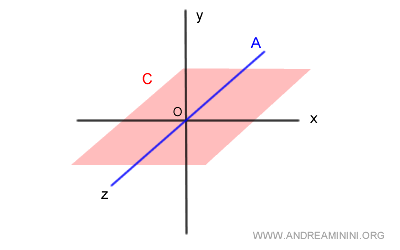
I calculate the intersection between A and C
$$ A \cap C=\{ R \} <> \{ 0_v \}$$
The intersection set A∩B consists of the infinite points of the Z-axis (blue). It's different from { 0v }.
Therefore, in this case the subspaces A and C are not in direct sum with each other.
Not being in direct sum, the subspaces A+V are not complementary subspaces.
It is therefore unnecessary to check if the sum A+C equals V.
And so on.
