Vector Subspace

What is a Vector Subspace?

A vector subspace is a subset of a vector space that fulfills all the properties of vector spaces.

Defining Vector Subspace

Let V be a vector space over a field K. A subset is a vector subspace of V $$ W ⊆ V $$ if it satisfies the following properties:
1. For any two elements w₁ and w₂ in W, their sum w₁+w₂ also belongs to W $$ \forall \ \vec{w}_1 \ , \ \vec{w}_2 \ \in \ W \ \Rightarrow \ \vec{w}_1 + \vec{w}_2 \in W $$
2. For any scalar λ from field K and any element w in W, the product λw also belongs to W. $$ \forall \ \lambda \in K \ , \ \forall \vec{w} \ \in \ W \ \Rightarrow \ \lambda \cdot \vec{w} \ \in \ W $$

In other words, a vector subspace is a subset closed under addition and scalar multiplication operations.

A vector subspace is itself a vector space.

Therefore, all properties of vector spaces hold true in a vector subspace.

Note. This aspect is crucial because not all subsets of a vector space are vector subspaces. To determine if a subset is a vector subspace, one must verify if it satisfies the properties of vector spaces.

How to Determine if a Subset is a Vector Space

To ascertain if a subset is also a vector space, check if the subset includes the zero element or not.

Why is this important?

The zero element is one of the properties of vector spaces.

Since a vector subspace is also a vector space, it must contain the zero element.

If a subset lacks a zero element, it is not a vector subspace.

Once it's established that the subset includes the zero element, check if it adheres to the properties of vector subspaces.

A subset is a vector subspace if it upholds the two properties of vector subspaces.

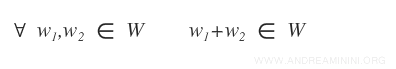
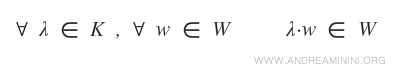
Therefore, calculate the sum of two elements in the subset and the scalar product of two generic vectors in the subset W.

If the result of the sum and scalar product still belongs to the subset W, then the subset is a vector subspace. Otherwise, it is not.

A Practical Example

Example 1

In this straightforward example, I'll determine whether a subset W is a vector subspace.

Example 2

In this next example, I examine another subset.

This time, the equation equals one, leading to a completely different outcome.

More Worked Examples

1. exercise 1
2. exercise 2
3. exercise 3
4. exercise 4
5. exercise 5
6. exercise 6

Identifying Vector Subspaces Through Graphical Analysis

I can also assess the properties of vector subspaces by observing their graphical representation on a Cartesian plane.

If subset W includes the zero element (0,0), the graph will intersect the origin O.

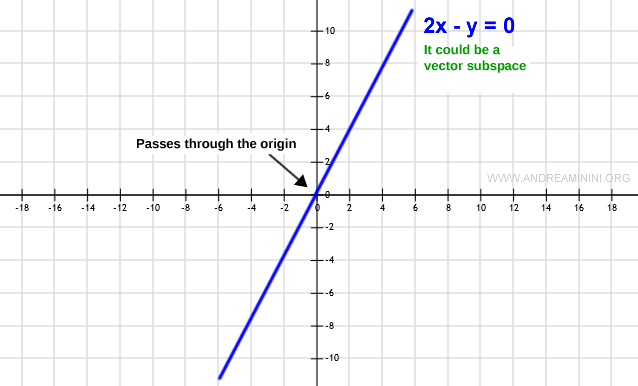
Note. This is a necessary but not sufficient condition. Even if the line passes through the origin, it doesn't necessarily mean it's a vector subspace. It could be, or it might not be.

If, on the other hand, the graph doesn’t pass through the origin, then subset W lacks the zero element.

Thus, subset W is not a vector subspace.

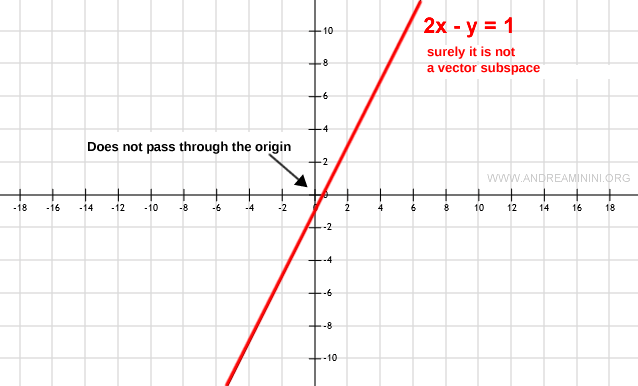
Note. If the line doesn’t pass through the origin, there’s no need for further verification. Certainly, subset W is not a vector subspace.

Once it's established that the line passes through the origin, I need to check if subset W adheres to the two properties of subspaces.

It's a vector subspace if...

Subset W is a vector subspace if the sum of any two elements is always a point on the line (subset W).

 

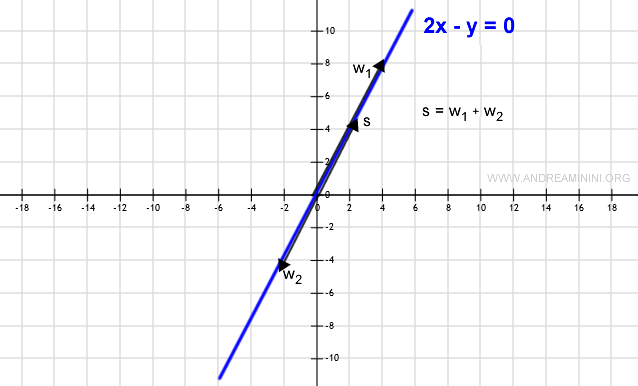
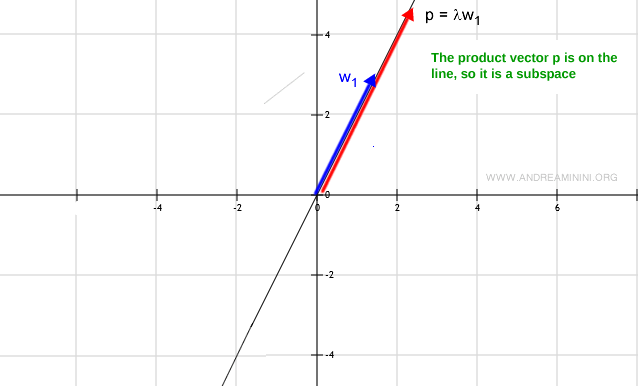
Additionally, given any scalar and an element w, the scalar multiplication always results in a vector on the line (subset W).

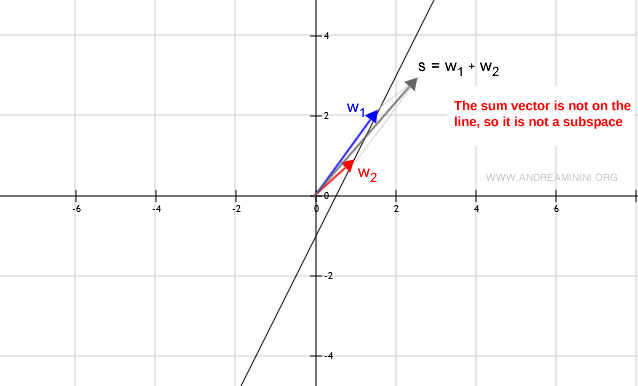
It's not a vector subspace if...

It's not a vector subspace if the sum w₁+w₂ results in a vector outside the line (subset W).

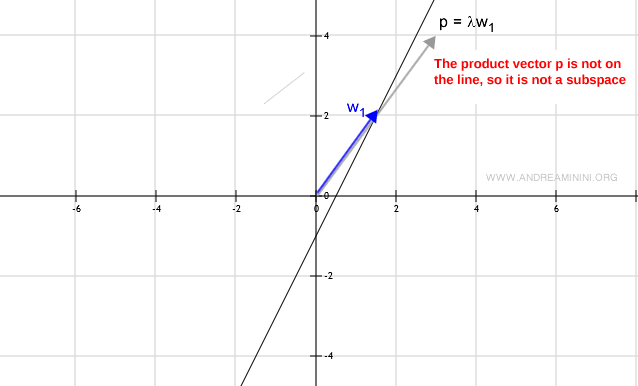
Or, given any element w, the scalar multiplication λw results in a vector outside the line (subset W).

In conclusion, graphical analysis on a plane also allows us to discern the properties of vector subspaces.

Vector Subspaces and Linear Combinations

A subset W of the vector space V is a vector subspace of V if its linear combination with n scalars also belongs to W.

This definition encapsulates the two characteristics of vector subspaces, namely closure with respect to addition and scalar multiplication.