The Union of Vector Subspaces

The union of two vector subspaces is not a vector subspace.

Consider V, a vector space in the field K, with A and B as two of its vector subspaces. Generally, the union of these subspaces, A ∪ B, does not form a vector subspace.

Why is that?

The union A ∪ B is not closed under addition.

$$ a+b \notin A \cup B $$

It is only closed under scalar multiplication.

$$ k \cdot a \in A \cup B $$

The Proof

Given two vector subspaces A and B, the task is to determine if their union A ∪ B constitutes a vector subspace.

$$ A \cup B $$

According to the first property of subspaces, for any two generic vectors a and b in the set A ∪ B, the sum a+b also belongs to A ∪ B.

$$ \forall \ \vec{a} \in A , \vec{b} \in B \Rightarrow \vec{a}+\vec{b} \in A \cup B $$

However, this is not always true.

Therefore, the proposition is false. 

A Practical Example

Let V be the vector space R².

For instance, the two-dimensional x,y plane consists of R·R points ( R² ) and serves as a practical example of the vector space R².

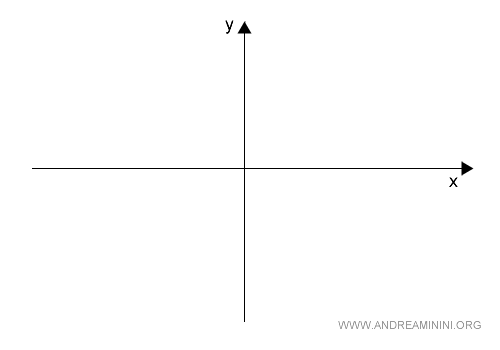
Consider two vector subspaces X and Y.

For example, the x-axis and the y-axis.

$$ X = \{ \binom x y \in R^2, y=0 \} $$

$$ Y = \{ \binom x y \in R^2, x=0 \} $$

The X and Y axes are both vector subspaces of the plane V as they are homogeneous linear systems.

Note. Being one-dimensional subspaces, they also facilitate graphical representation, making the explanation of concepts clearer.

 

The union X∪Y comprises the vectors on the X axis and the Y axis (in blue).

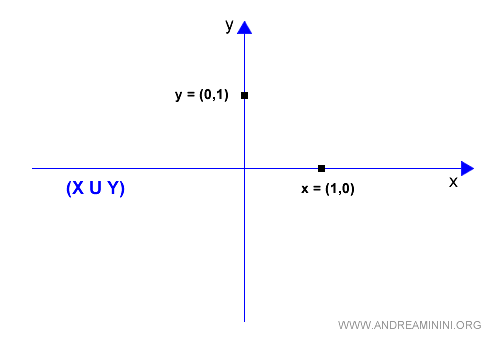
The union X∪Y is not a vector subspace because it is not always closed with respect to the addition of two generic elements x+y.

To demonstrate this, I'll use a counterexample.

Consider two vectors

$$ \vec{x} \in X $$

$$ \vec{y} \in Y $$

For example

$$ \vec{x}=\begin{pmatrix} 1 \\ 0 \end{pmatrix} $$

$$ \vec{y}=\begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

Add them together x+y.

The sum equals x+y

$$ \vec{x}+\vec{y} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$

Now, let's verify if the sum of the two vectors is included in the union X∪Y, as this is one of the properties of vector subspaces.

$$ \vec{x}+\vec{y} \in X \cup Y $$

Geometrically, it's immediately apparent that the sum of the vectors x+y does not belong to the union X∪Y, since the point (x,y)=(1,1) lies outside both vector spaces (X axis + Y axis).

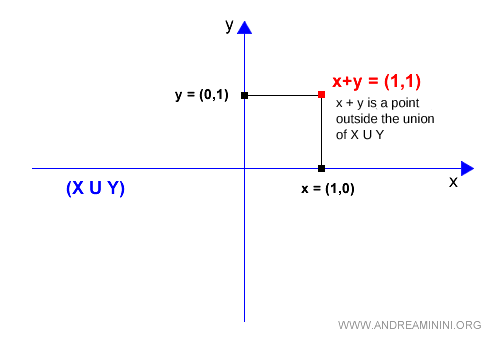
Substituting the sum x+y

$$ X = \{ \binom 1 1 \in R^2, y=0 \} $$

$$ Y = \{ \binom 1 1 \in R^2, x=0 \} $$

Thus

$$ X = \{ \binom 1 1 \in R^2, 1=0 \} $$

$$ Y = \{ \binom 1 1 \in R^2, 1=0 \} $$

Both are not true (false).

Therefore, the sum x+y is not included in the union X∪Y.

$$ \vec{x}+\vec{y} \notin X \cup Y $$

The union of two vector subspaces does not satisfy the sum property of vector spaces.

Note. The union of vector subspaces only satisfies the scalar multiplication property, as kx ∈ X∪Y. However, this is not sufficient to define a vector subspace. Both properties must be satisfied.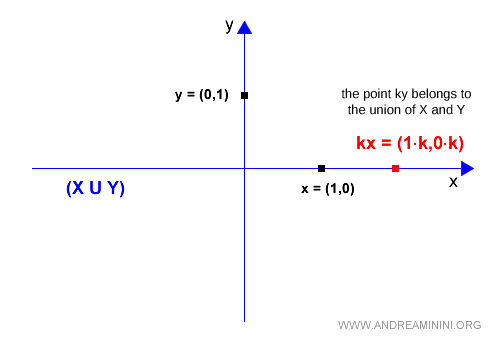

This demonstrates that generally, the union of two vector subspaces is not a vector subspace.

The Smallest Vector Subspace Encompassing the Union of Subspaces

The sum of vector spaces A+B is the smallest vector subspace of V that encompasses the union of the subspaces A∪B.

Proof

In a vector space V, consider two vector subspaces A and B

$$ A,B \subseteq V $$

Let's consider a generic vector subspace L that contains both A and B, that is, the union of the two subspaces A∪B.

$$ A \cup B \subseteq L \subseteq V $$

As L is a vector subspace, by definition, it includes the sum of vectors within L.

Consequently, it also includes the sum of vectors from A and B

$$ \{ \vec{a}+\vec{b} \ | \ \vec{a} \in A, \ \vec{b} \in B \} \subseteq L $$

Therefore, the vector subspace L encompasses the sum of the vector subspaces A+B

$$ A+B \subseteq L $$

In general, any vector subspace that contains A and B also includes their sum A+B.

The sum of the vector subspaces A+B is itself a vector subspace (see proof).

Therefore, among all vector subspaces that encompass the union of the subspaces A∪B, the sum subspace A+B is the smallest.

Explanation. The subspace A+B is contained within all subspaces that include A and B, namely the union A∪B. Therefore, A+B is definitively the smallest among all the vector subspaces of V that encompass the union of the subspaces A∪B.

Observations

Some observations on the union of vector subspaces:

• Generally, the union of two vector subspaces is not a vector subspace. However, in certain special cases, the union of vector subspaces can be a subspace. For example, if one of the vector subspaces is contained within the other $$ X \subset Y $$, then the union is also a vector subspace because it coincides with the subspace Y. $$ X \cup Y = Y $$

And so on.