Vector Subspace Exercise 3
Let $V = \mathbb{R}^2$, and consider the subset: $$ W = \{ (x, y) \in \mathbb{R}^2 \mid x^2 - y = 0 \} $$ We are asked to determine whether $W$ is a vector subspace of $V$.
To qualify as a subspace, $W$ must satisfy all the axioms of a vector space, including closure under vector addition and scalar multiplication, and it must contain the zero vector.
1) The Zero Vector
Consider a generic vector $\vec{w} = \begin{pmatrix} x \\ y \end{pmatrix}$ in $W$. By definition,
$$ \vec{w} \in W \quad \Leftrightarrow \quad x^2 - y = 0 $$
Let’s check whether the zero vector $\begin{pmatrix} 0 \\ 0 \end{pmatrix}$ belongs to $W$:
$$ (0)^2 - 0 = 0 $$
Since the condition is satisfied, the zero vector is in $W$.
Note. Verifying that the zero vector is included is a crucial first step. If it’s missing, the set cannot be a vector space and therefore cannot be a subspace. In such cases, the verification ends immediately.
2) Closure Under Vector Addition
Now let’s examine whether $W$ is closed under addition. Take two arbitrary vectors in $W$:
$$ \vec{w}_1 = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}, \quad \text{with } x_1^2 - y_1 = 0 $$
$$ \vec{w}_2 = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix}, \quad \text{with } x_2^2 - y_2 = 0 $$
We compute their sum and check if it also belongs to $W$:
$$ \vec{w}_1 + \vec{w}_2 = \begin{pmatrix} x_1 + x_2 \\ y_1 + y_2 \end{pmatrix} $$
Substitute into the defining condition:
$$ (x_1 + x_2)^2 - (y_1 + y_2) = x_1^2 + 2x_1x_2 + x_2^2 - y_1 - y_2 $$
Group terms:
$$ = (x_1^2 - y_1) + (x_2^2 - y_2) + 2x_1x_2 $$
Since $x_1^2 - y_1 = 0$ and $x_2^2 - y_2 = 0$, the expression simplifies to:
$$ 0 + 0 + 2x_1x_2 = 2x_1x_2 $$
This equals zero only when $x_1 = 0$ or $x_2 = 0$, but not in general.
Therefore, $\vec{w}_1 + \vec{w}_2$ does not necessarily belong to $W$:
$$ \vec{w}_1 + \vec{w}_2 \notin W $$
So $W$ is not closed under vector addition, and hence fails to satisfy a fundamental requirement for subspaces.
We conclude that $W$ is not a vector subspace of $\mathbb{R}^2$.
Note. Geometrically, the equation $x^2 - y = 0$ defines a parabola, not a straight line. The sum of two vectors lying on a parabola will, in general, fall outside the parabola - unless one of the vectors is the zero vector.
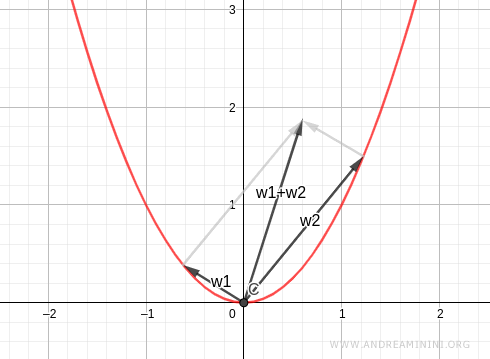
And so on.
