Linear Span

The term linear span refers to a set of n vectors v₁, v₂, ..., v_n in a vector space V over a field K, which generates a subspace of V through linear combinations with scalars α₁, α₂, ..., α_n from K. $$ Span( v_1 ,..., v_n ) = \{ α_1 \cdot v_1 ,..., α_n \cdot v_n \: \: \forall α_i \in K \} $$

A linear span is also denoted by the symbols L_k, L or <>.

$$ L_k ( v_1 ,..., v_n ) $$ $$ L( v_1 ,..., v_n ) $$ $$ < v_1 ,..., v_n > $$

The Span(v₁, ..., v_n) forms a subspace of the vector space V.

It is known as the subspace generated by vectors v₁, ..., v_n.

Practical Examples

Example 1

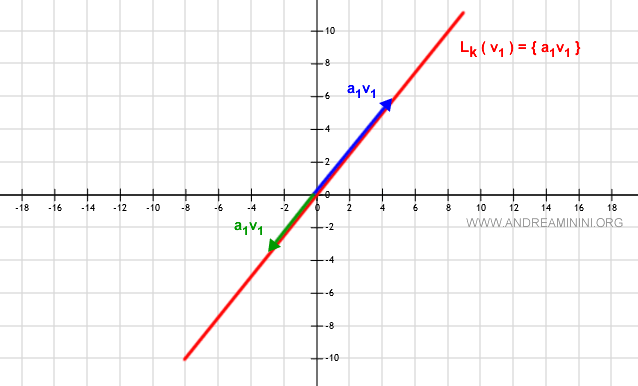
If a vector v₁ in the vector space V over the field R² is non-zero ( v₁≠Ø ), then its linear span L(v₁) comprises all vectors α₁v₁ for every α₁∈R, lying on the line through the origin in the direction of v₁.

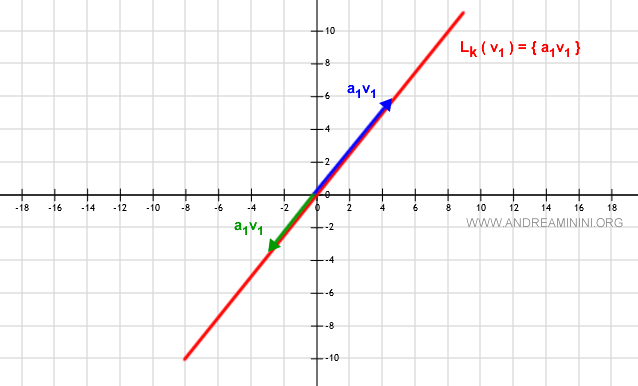
Each value of α₁∈R generates a vector α₁v₁ on the line L_k, in the same direction but of varying length, each a multiple of v₁.

It's immediately apparent that L_k is a vector subspace of V.

Example 2

Given two vectors v₁ and v₂ in the vector space V over the field R², the linear span L_k(v₁, v₂) consists of all vectors α₁v₁ + α₂v₂ for every α₁, α₂∈R originating in the plane.

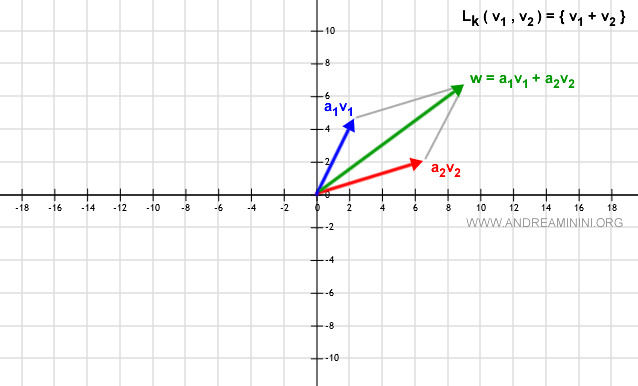
Each pair of values α₁, α₂∈R generates a vector w= α₁v₁ + α₂v₂ with different direction, orientation, and length.

If the two vectors are non-parallel, the vector w is determined by the parallelogram rule as a sum of a multiple of the vector v₁ and a multiple of the vector v₂.

Similarly, in this scenario, L_k(v₁+v₂) forms a vector subspace of V.

Note. If the two vectors are parallel, it reverts to the case of the line through the origin. Here, the two vectors share the same direction and lie on the same line . Thus α₁v₁+α₂v₂ are multiples of the same vector. It’s akin to writing α₁v₁. In fact, if the vectors are parallel, we have L(v₁,v₂) = L(v₁).