The Intersection of Vector Subspaces

The intersection of two vector subspaces is itself a vector subspace.

Let V be a vector space over the field K, with A and B as two of its vector subspaces. The intersection A∩B is a subspace of V.

Proof

Consider a vector space V and its two vector subspaces A and B.

I aim to prove that the intersection of the vector subspaces A∩B is also a vector subspace.

To do this, I'll check if the intersection meets all the criteria for vector subspaces.

Note: A vector subspace must contain the zero vector and be closed under vector addition and scalar multiplication.

1) Presence of the Zero Element

The zero vector is present in both A and B.

$$ \vec{0} \in A $$

$$ \vec{0} \in B $$

Therefore, the zero vector is in the intersection of A∩B.

$$ \vec{0} \in A∩B $$

Thus, it's not ruled out that the intersection A∩B is a vector subspace.

I need to continue and verify the other properties of vector subspaces.

2) Closure under Vector Addition

Take any two vectors from the intersection of the two subspaces A∩B.

$$ \vec{a}, \vec{b} \in A∩B $$

Both vectors a and b belong to the subspaces A and B since they are from the intersection A∩B.

$$ \vec{a}, \vec{b} \in A $$

$$ \vec{a}, \vec{b} \in B $$

As A and B are vector subspaces, they are closed under addition and multiplication.

Thus, the sum of vectors a and b belongs to the vector subspace A.

$$ \vec{a} + \vec{b} \in A $$

Similarly, the sum of vectors a and b belongs to the vector subspace B.

$$ \vec{a} + \vec{b} \in B $$

The sum a+b is present in both A and B.

Hence, the sum of the two vectors belongs to the intersection A∩B.

$$ \vec{a} + \vec{b} \in A∩B $$

This demonstrates that the intersection of two subspaces is closed under addition.

This property of vector subspaces is thus satisfied.

3) Closure under Scalar Multiplication

Consider any vector v from the intersection of the two vector subspaces A∩B.

$$ \vec{v} \in A∩B $$

Then take any scalar λ from the field K.

$$ \lambda \in K $$

The vector v belongs to both subspaces A and B as it's from the intersection A∩B.

$$ \vec{v} \in A $$

$$ \vec{v} \in B $$

Since A and B are vector subspaces, they are closed under scalar multiplication of any vector.

Therefore, the product of vector v and scalar λ belongs to both subspaces A and B.

$$ \lambda \cdot \vec{v} \in A $$

$$ \lambda \cdot \vec{v} \in B $$

Consequently, the scalar product belongs to the intersection A∩B.

I have thus proven that the intersection A∩B is closed under scalar multiplication.

This property of vector subspaces is confirmed.

In Conclusion

The intersection of two subspaces contains the zero vector and is closed under both vector addition and scalar multiplication. Therefore, the intersection of two subspaces A∩B is a vector subspace.

The intersection A∩B is a vector subspace of both A and B.

And naturally, the intersection A∩B is also a vector subspace of the vector space V itself.

A Practical Example

The xy Cartesian plane is a vector space V over the field K=R².

It's a two-dimensional plane RxR.

The X and Y axes are two vector subspaces of the space V.

Both subspaces are homogeneous linear systems and include the null element.

$$ X = \{ \binom x y \in R^2, y=0 \} $$

$$ Y = \{ \binom x y \in R^2, x=0 \} $$

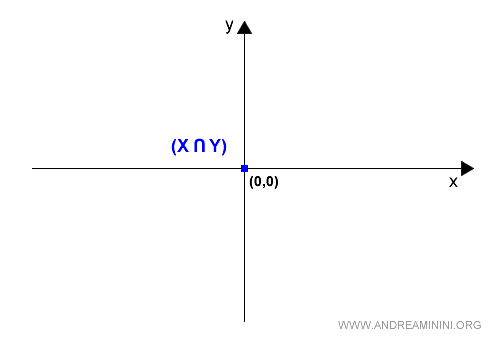
The intersection X⋂Y of the Cartesian axes is as follows:

$$ X \cap Y = \{ \binom x y \in R^2, x=0, y=0 \} $$

Practically, the intersection X⋂Y contains only the null vector.

$$ X \cap Y = \{ \vec{0} \} $$

Note. This does not mean that the intersection is empty X⋂Y=Ø. The intersection is not empty X⋂Y≠Ø because it contains a vector X⋂Y={0}, namely the null vector.

Graphically, the intersection is the origin point O (blue) of the Cartesian diagram.

The presence of the null vector does not allow us to exclude that X⋂Y is a vector space.

We must verify the other properties of vector subspaces.

Property 1 (closure with respect to vector addition)

Consider any two vectors from the intersection X⋂Y

$$ \vec{x} \in X $$

$$ \vec{y} \in Y $$

The sum of the vectors equals x+y

$$ \vec{x}+\vec{y} $$

We need to determine whether the sum vector is included in the intersection X⋂Y.

$$ X \cap Y = \{ \binom x y \in R^2, x=0, y=0 \} $$

The intersection X⋂Y contains only the null vector.

$$ X \cap Y = \{ \vec{0} \}$$

Therefore, the vectors x and y are both the null vector.

$$ \vec{x}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

$$ \vec{y}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

The sum of the null vector with itself is always the null vector.

$$ \vec{x} + \vec{y}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0+0 \\ 0+0 \end{pmatrix} =\begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

Thus, the sum of the vectors x+y is included in the intersection X⋂Y.

$$ \vec{x}+\vec{y} =\begin{pmatrix} 0 \\ 0 \end{pmatrix} \in X \cap Y $$

The first property of vector subspaces is satisfied.

Property 2 (closure with respect to scalar multiplication of a vector)

To verify the second property of subspaces, consider a scalar k and a vector x from the intersection of the subspaces X⋂Y.

$$ \vec{x} \in X⋂Y $$

$$ k \in R $$

We need to check if the scalar multiplication of the vector belongs to the intersection X⋂Y.

$$ X \cap Y = \{ \binom x y \in R^2, x=0, y=0 \} $$

The intersection X⋂Y contains only the null vector.

$$ X \cap Y = \{ \vec{0} \}$$

Therefore, the vector x is necessarily the null vector.

$$ \vec{x}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

Any scalar k multiplied by the null vector results in the null vector itself.

$$ k \cdot \vec{0} = k \cdot \begin{pmatrix} 0 \\ 0 \end{pmatrix} = \begin{pmatrix} k \cdot 0 \\ k \cdot 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} = \vec{0} $$

Thus, the scalar product belongs to the intersection X⋂Y.

$$ k · \vec{0} \in X⋂Y $$

Even the second property of vector subspaces is satisfied.

In conclusion

The intersection of the X and Y axes is a vector subspace.

The intersection X⋂Y is a vector subspace of X and Y.

Additionally, the intersection X⋂Y is also a subspace of the vector space V, namely the Cartesian plane.

Observations

Some observations on the intersection of vector subspaces

• The intersection of two vector subspaces can never be an empty set $$ X \cap Y \ne Ø $$

  Proof. Since X and Y are vector subspaces, they both contain by definition the neutral element of addition, the null vector $$ \vec{0} \in X \ , \ \vec{0} \in Y \Rightarrow \vec{0} \in X \cap Y $$ Therefore, the intersection can never be empty because at least one vector (the null vector) belongs to it. Hence, it may happen that the intersection of the vector subspaces X⋂Y contains only the null vector $$ X \cap Y = \{ \vec{0} \} $$ However, it can never be the case that the intersection of the vector subspaces is an empty set $$ X \cap Y \ne Ø $$